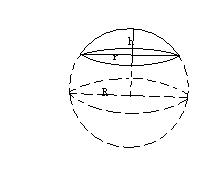
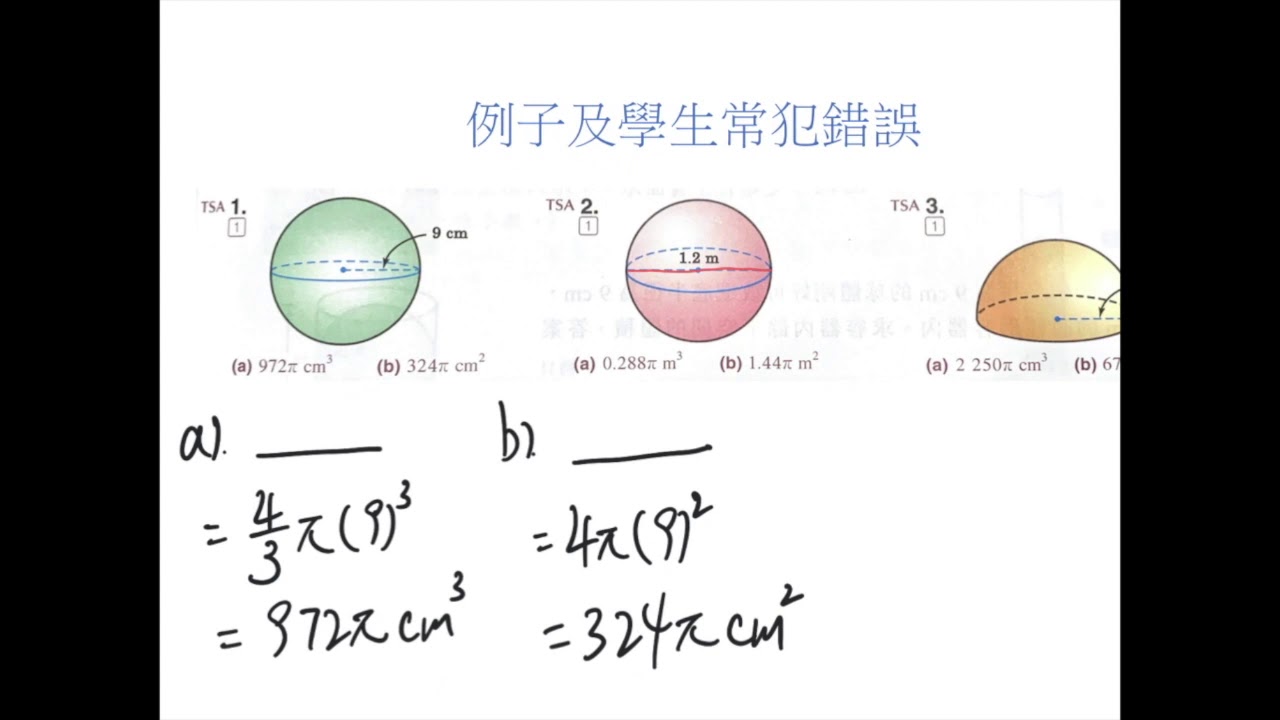
表面積は球の半分です。 表面積の公式に当てはめると、以下のように計算できます。 4 π × 4 2 × 1 2 = 32 π また、半球の断面図の面積を加えなければいけません。 円の面積の公式に当てはめると、以下のように計算できます。 4 × 4 × π = 16 π 面積の合計は以下のように 48 π cm 2 になります。 32 π 16 π = 48 π 公式を利用して球の問題を解く 中学数学で学ぶ分野の一つが球の体積と表面積です。
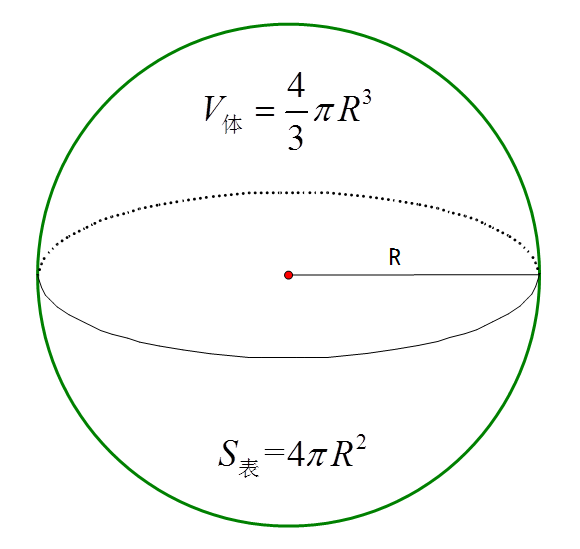
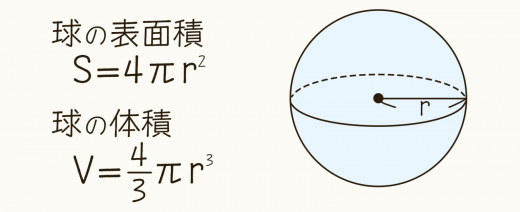
球体 表面積 体積 公式- 球の体積の公式をつかいましょう! 球の体積の公式は、4πr3 / 3でしたね。 4πr 3 / 3 にr=3を代入します。 4π×3 3 / 3 = 36π・・・(答) となります。 簡単ですよね? 球の体積の公式は必ず覚えましょう! 球の表面積に関する問題 下の図のように、半径3の半球があるとき、この球の表面積を求めよ。 解答&解説 半球(球を2等分したうちの片方)ということに注意しましょう!球の表面積を求める公式は、次の通りです。 S = 4πr2 S = 4 π r 2 ここで、S は球の表面積、π は円周率、r は球の半径を表します。 球の表面積を求めるには、この公式に球の半径 r を代入すればよいだけです。 このページの続きでは、例題を使って、この公式の使い方を説明しています。 もくじ 球の表面積を求める公式 球の表面積を求める計算問題 半径から球の表面積を求める問題 2種類の球の表面
球体 表面積 体積 公式のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  | |
 |  | |
「球体 表面積 体積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  |  |
 |  |  |
「球体 表面積 体積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 | ||
 |  | |
「球体 表面積 体積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
:max_bytes(150000):strip_icc():format(webp)/surface-area-1-589dd97c3df78c47588a9b3a.jpg) | ||
 |  |  |
 | ||
「球体 表面積 体積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  | |
 |  | |
「球体 表面積 体積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  |  |
「球体 表面積 体積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 | ||
 |  | |
 |  | |
「球体 表面積 体積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  | |
 | ||
「球体 表面積 体積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 | ||
 |
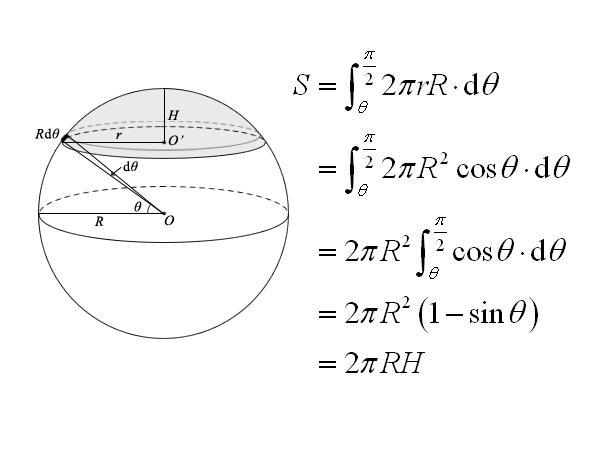
球の体積と表面積の公式の覚え方 以下の語呂合わせで覚える方法が有名です: 球の表面積: 4\pi r^2 4πr2 →「心配アール二乗」 球の体積: \dfrac {4} {3}\pi r^3 34 πr3 →「身の上に心配アール三乗」 意味はわからないかもしれませんが,何度も口に出していると自然と覚えます。 私も,球体の表面積や体積を求めるときは,今でも語呂で公式を思い出しています。 球の体積と表面積の 球体的表面积公式 球体表面积公式 S(球面)=4πr^2√表示根号 运用第一数学归纳法:把一个半径为R的球的上半球横向切成n份, 每份等高 并且把每份看成一个圆柱,其中半径等于其底面圆半径 则从下到上第k个圆柱的侧面积S(k)=2πr(k)×h 其中h=R/n ,r(k)=
Incoming Term: 球体表面積公式, 球体 表面積 公式 証明, 球体 表面積 公式 なぜ, 球体 表面積 公式 中学, 球体 表面積 体積 公式,




0 件のコメント:
コメントを投稿