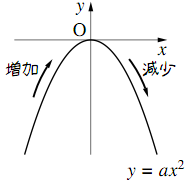
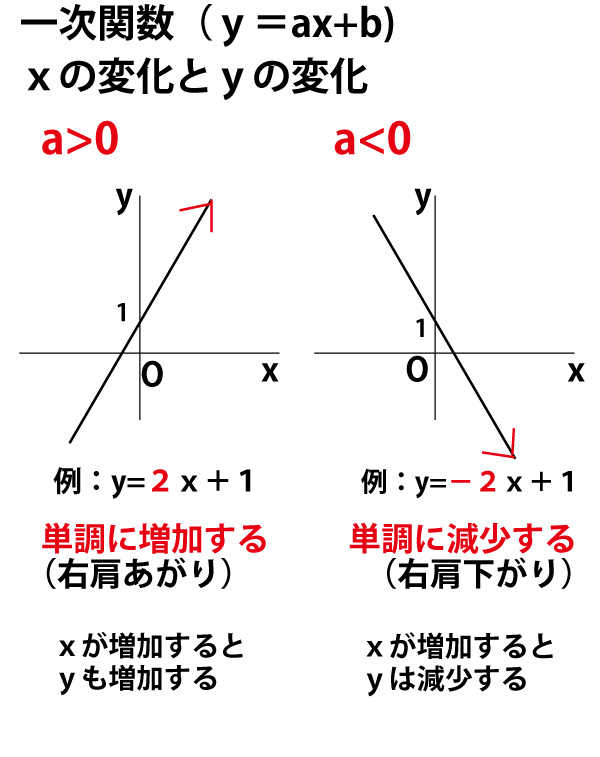
このページでは、二次関数のグラフを決定するのに必要な要素や、グラフの特徴について解説します。 ある二次関数のグラフを言葉だけで説明するとき、最もわかりやすいのは、 グラフの形と位置 について説明することだと思います。 では、グラフの形や位置と、 `y = ax^2 bx c` という式は
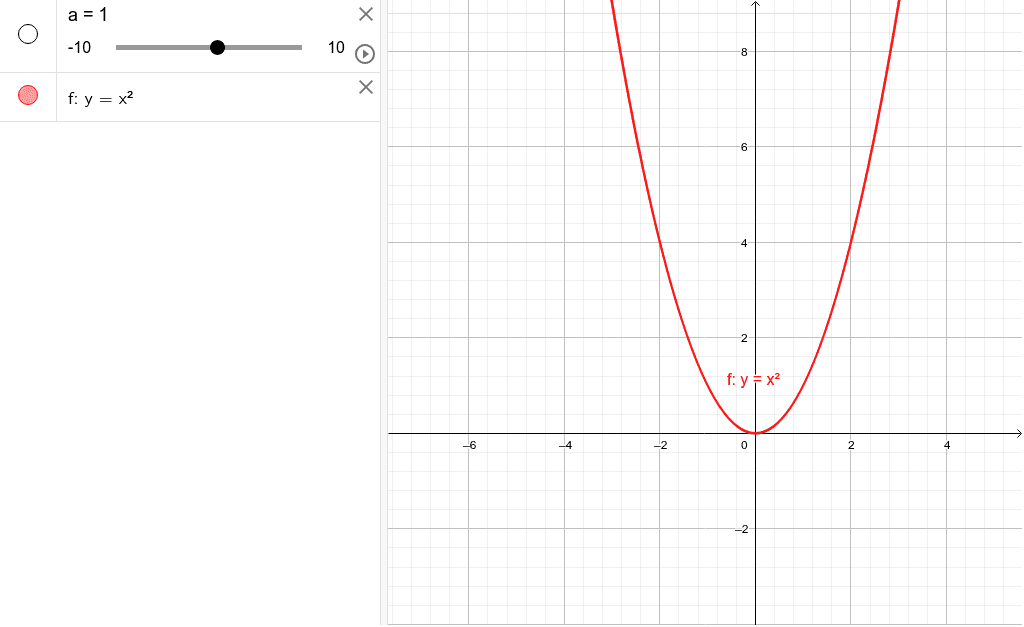
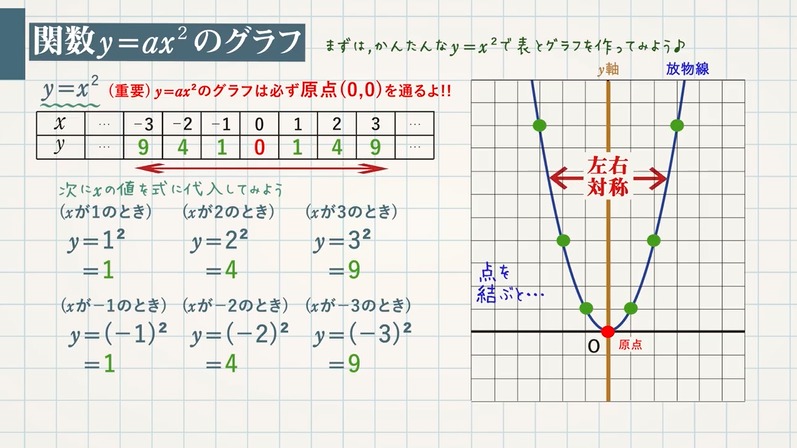
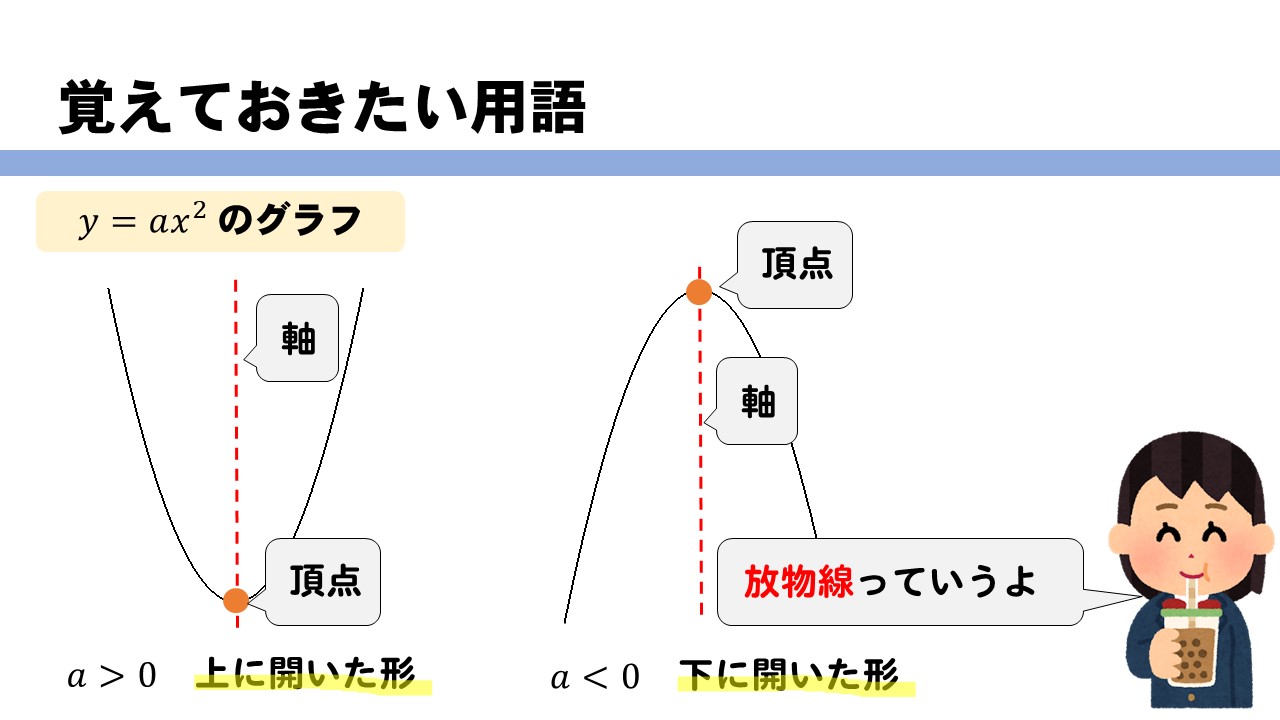
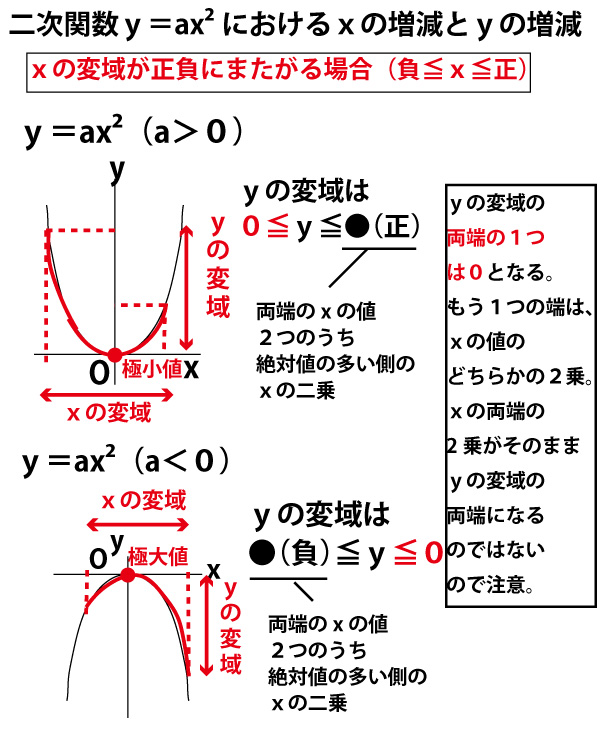
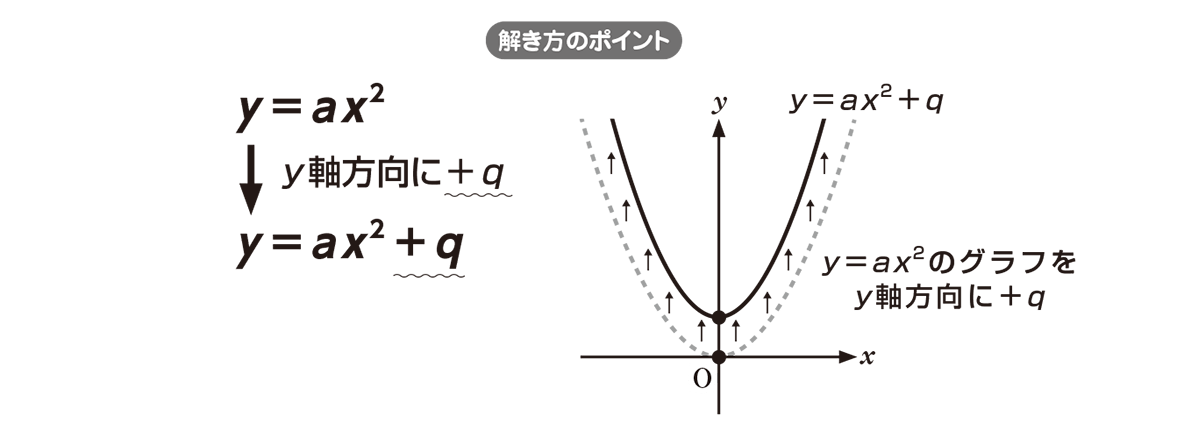
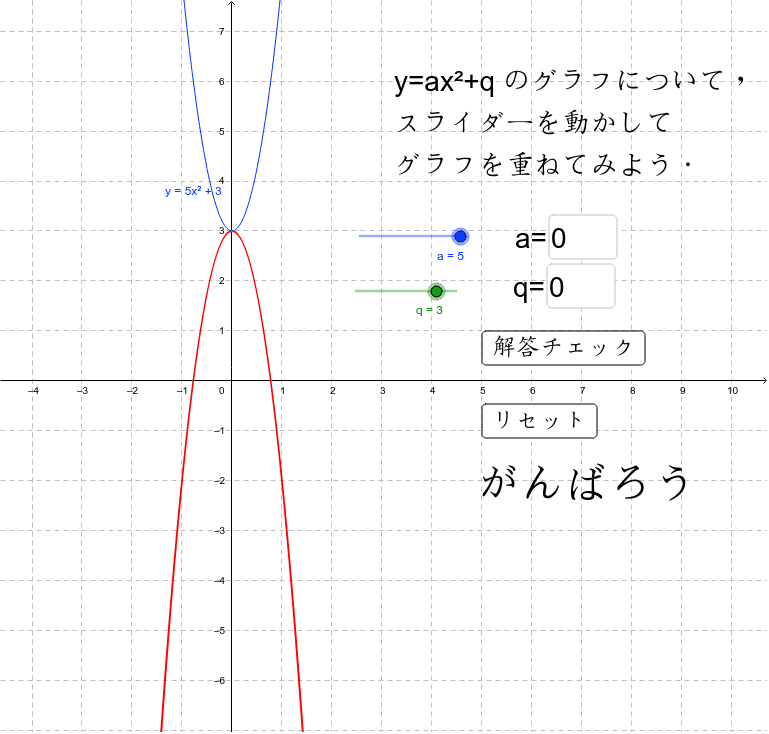
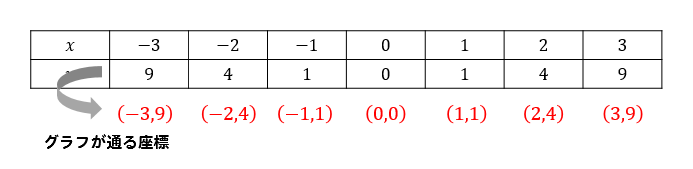
Y=ax二乗のグラフの特徴- 16年7月11日 年5月14日 基本二次関数 y=ax^2 のグラフ では、二次関数 y = ax2 y = a x 2 のグラフを見ました。 ここでは、この二次関数のグラフを上下に移動したものを考えていくことにします。 目次 平行移動 点の移動 二次関数 ax^2q のグラフ同様に y の値から x の値を求めることもできます。 ただし x の値は絶対値が同じで正と負の2つの値が算出されます。 これはグラフにするとわかりやすいと思いますが二乗に比例する関数のグラフは y 軸に対して対称な放物線となるため、同じ y の値となる点は2つあるためです。
Y=ax二乗のグラフの特徴のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 |  |  |
 |  | |
 |  | |
「Y=ax二乗のグラフの特徴」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
 |  |  |
「Y=ax二乗のグラフの特徴」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
 |  | |
「Y=ax二乗のグラフの特徴」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 |  | 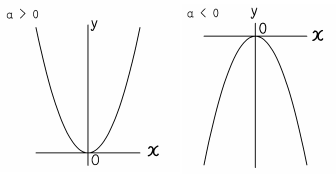 |
 |  |  |
「Y=ax二乗のグラフの特徴」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  | |
「Y=ax二乗のグラフの特徴」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
 |  |  |
「Y=ax二乗のグラフの特徴」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 | ||
 |  | |
「Y=ax二乗のグラフの特徴」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
 | ||
「Y=ax二乗のグラフの特徴」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |
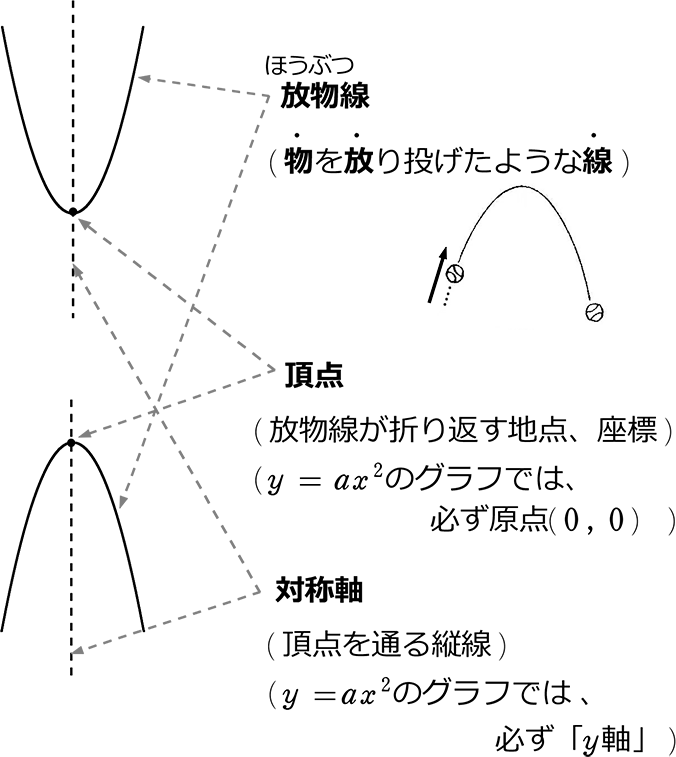
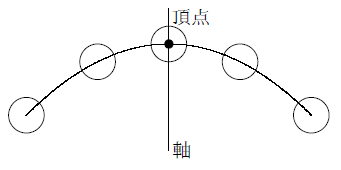
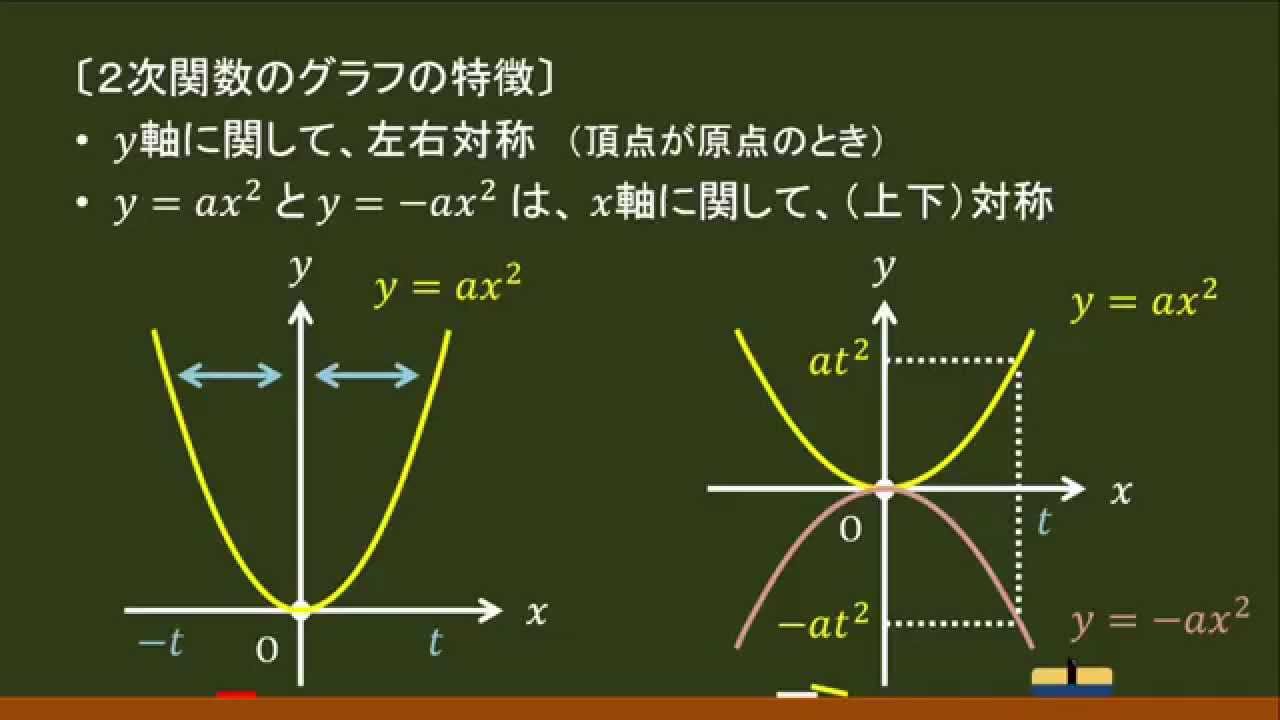
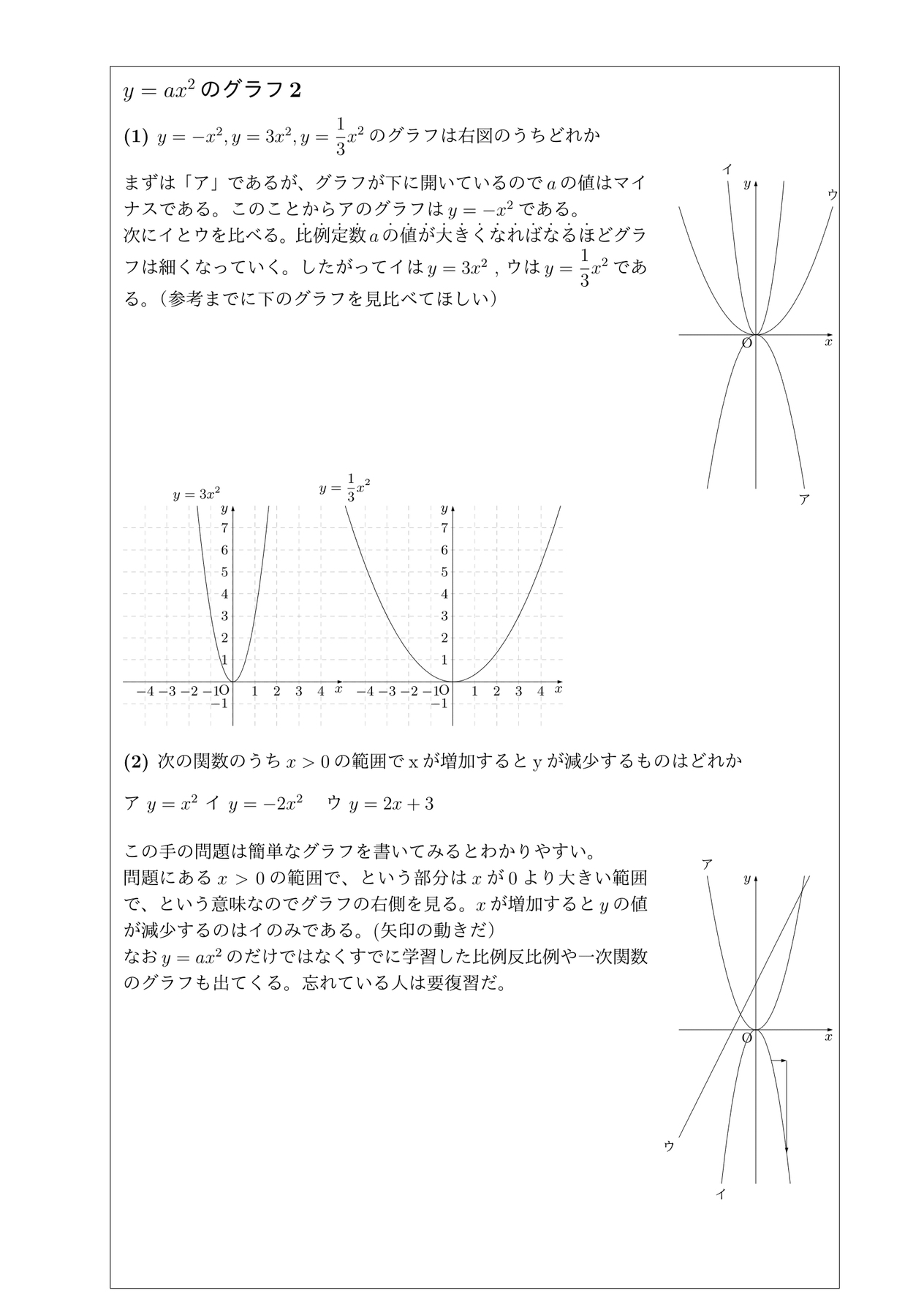
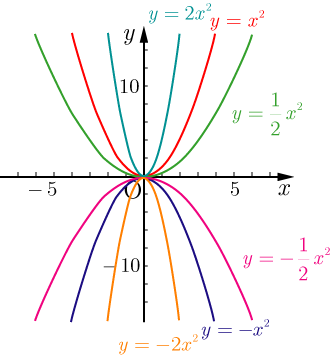
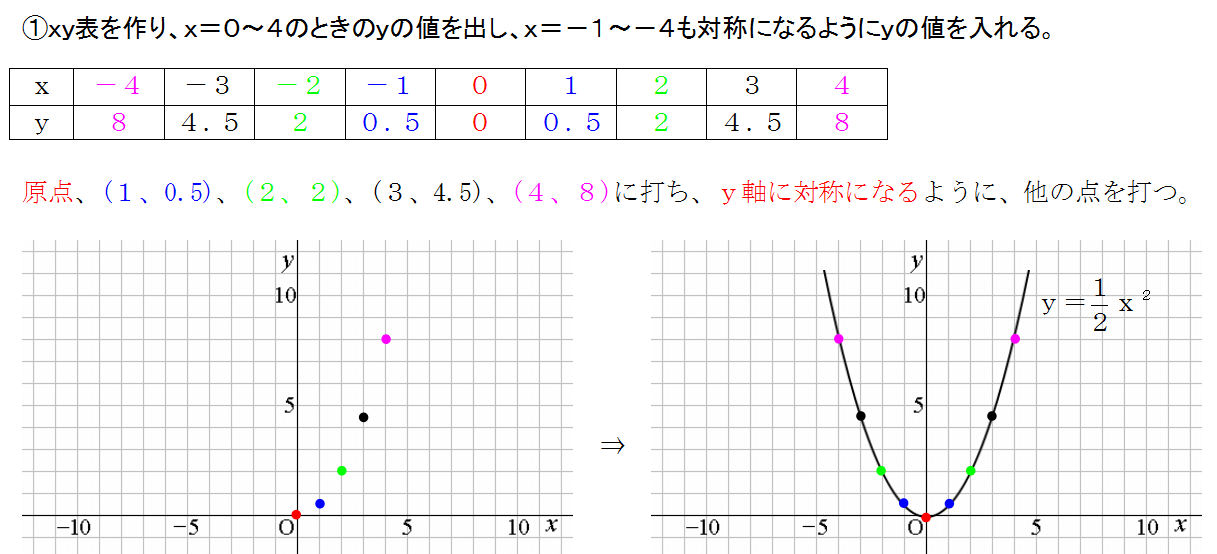
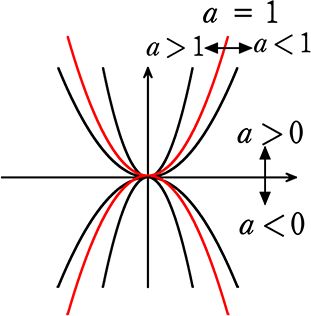
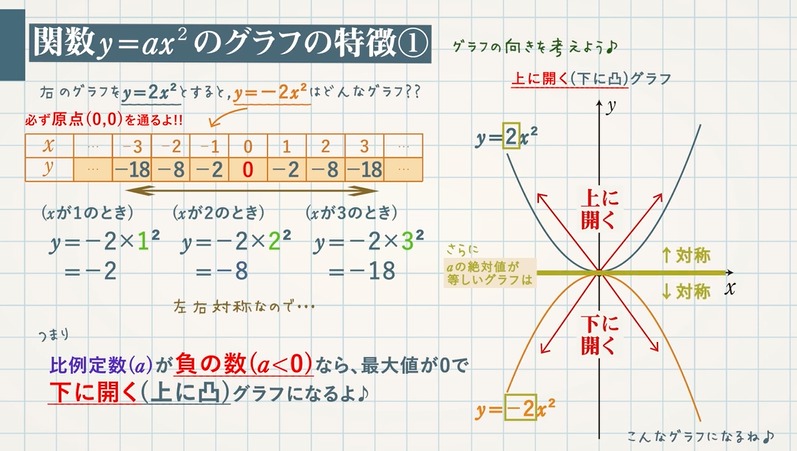
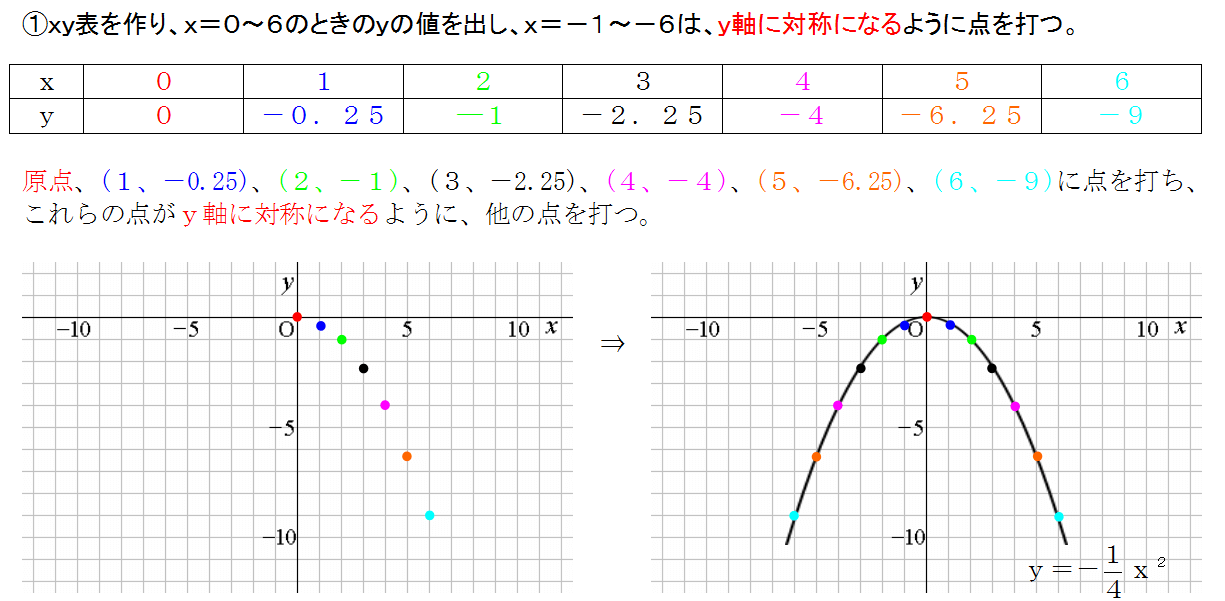
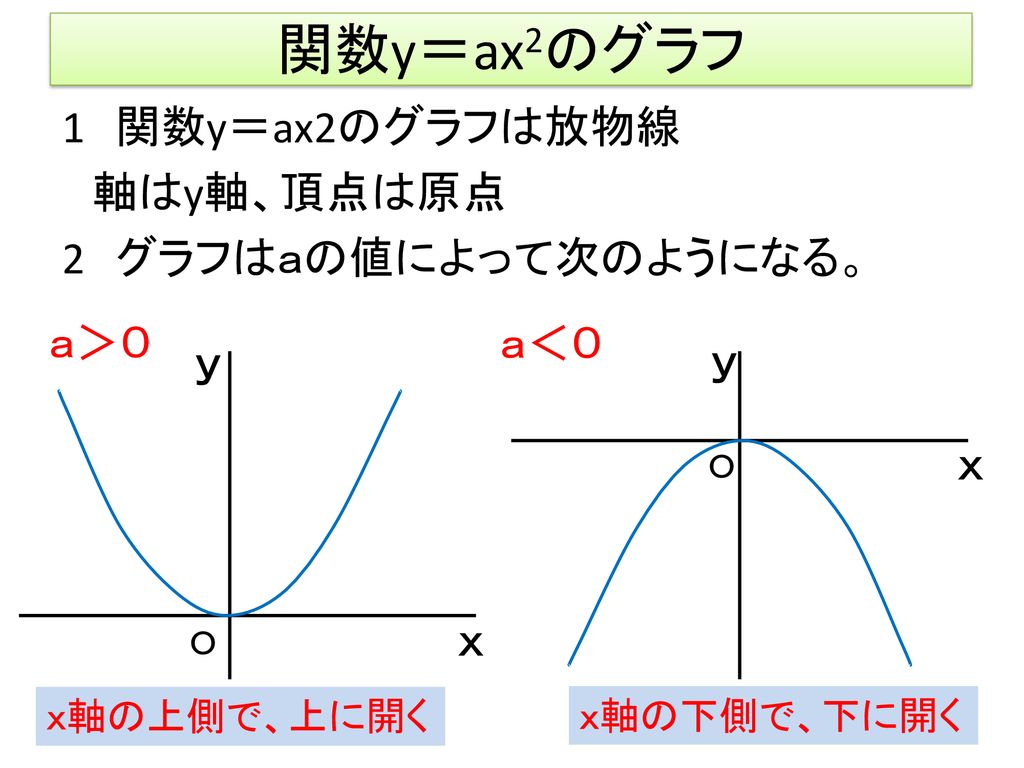
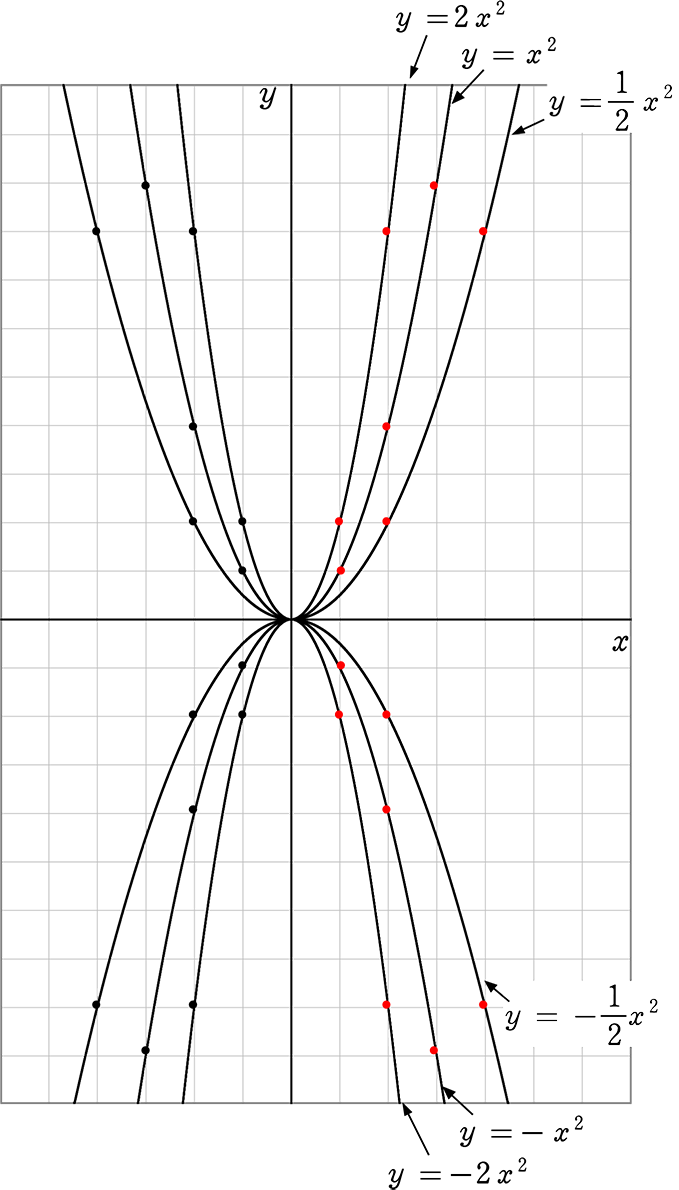
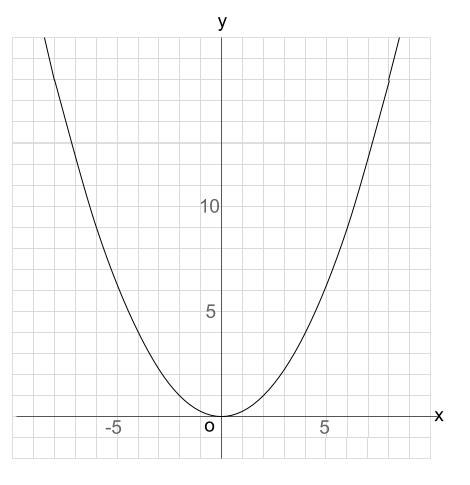
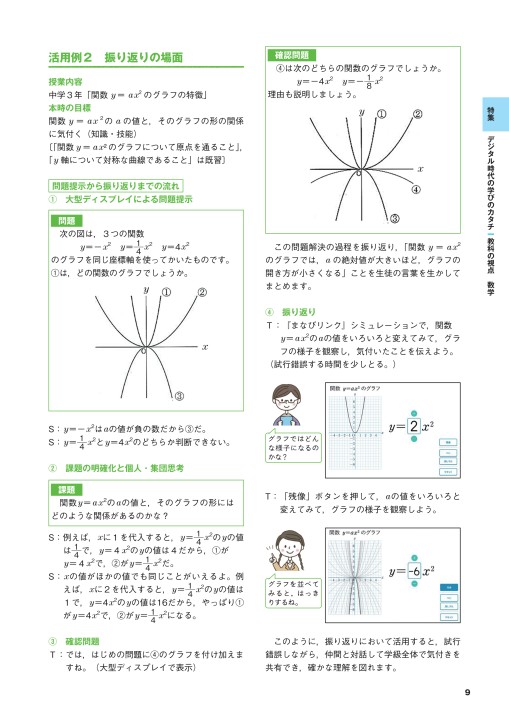
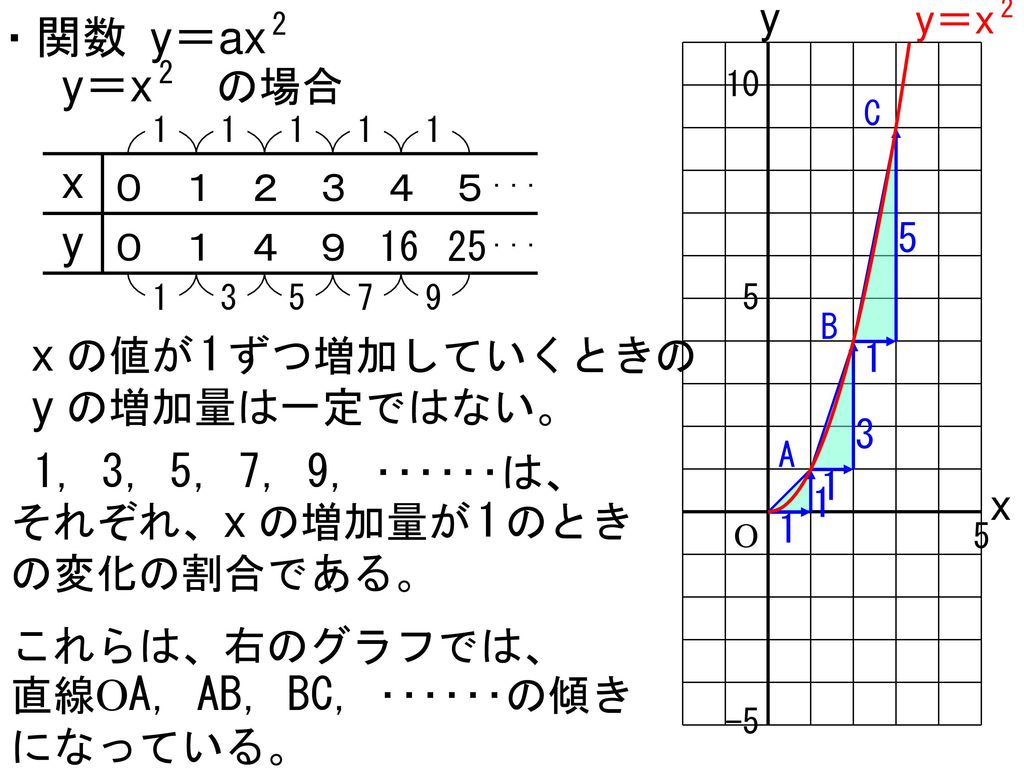
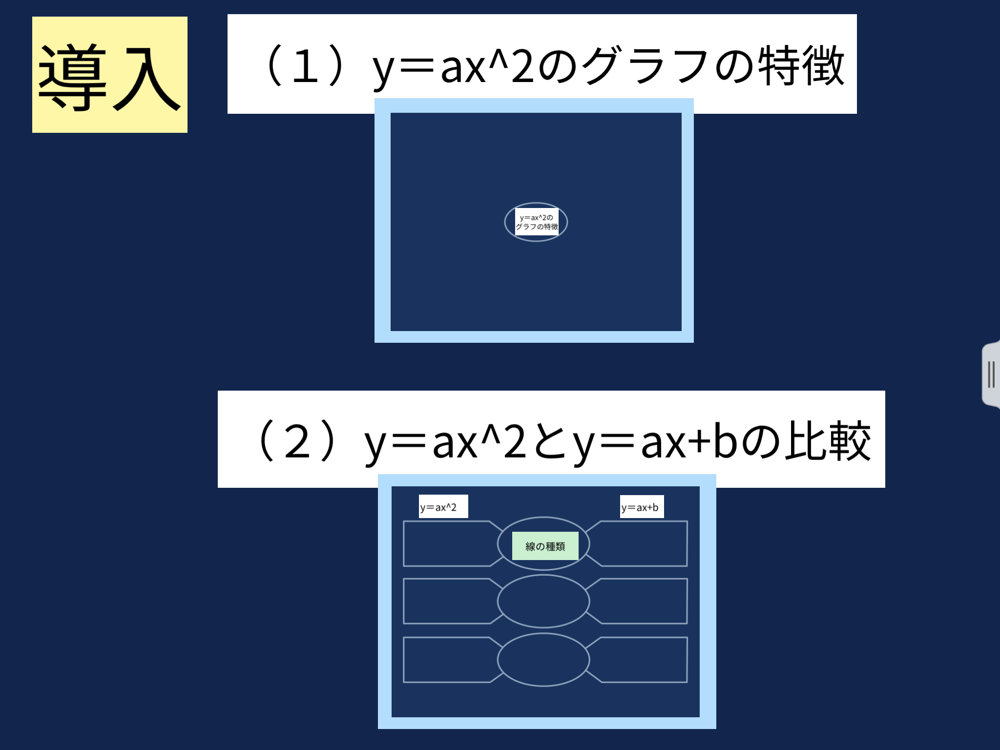
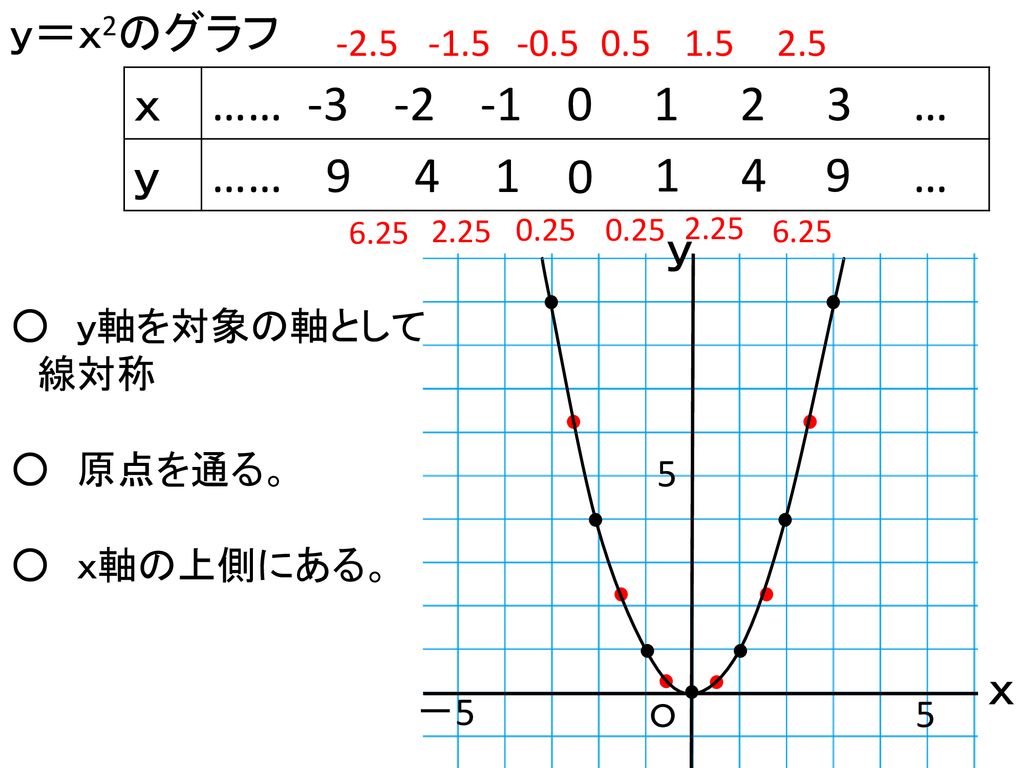
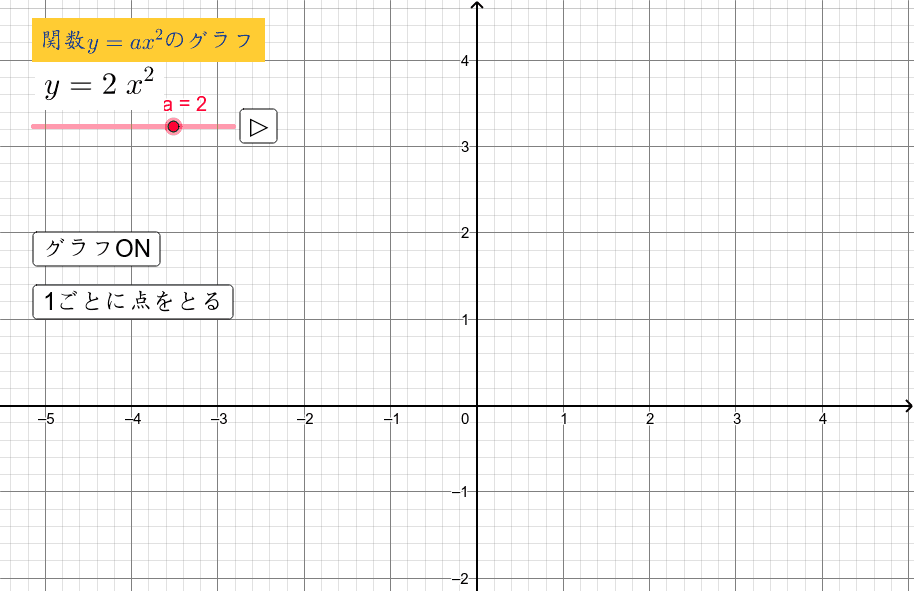
VMA03 2 2 乗に比例する関数のグラフ ここでは,関数y=ax2 のグラフとその特徴について学習してみましょう。 関数y=ax2 において,x=k,-kのときのyの値をそれぞれ求 めると,ともに y=ak2, ya k ak=-=_i2 2 となるから, y=ax2 のグラフは 軸に関して対称であるといえます。Y=ax2 のグラフ の特徴を理解し 平成29年度佐賀県教育センター 中学校数学科教育 学習指導案①3 y=ax2 のグラフを かくことができ る。 ・方眼のないグラフ 考えることがで きる。 ている。 4 で,y=ax2 のa の 値の違いから式 とグラフの対応 を判断する。 a の値の違いか ら式とグラフの 対応を





0 件のコメント:
コメントを投稿