動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru 円すいの展開図、側面積の求め方! 公式を使って15秒で解こう♪ 面積 面積 この円すいの側面積を求めなさい。 円周率は314とします。 知りたがりT:a=底面の面積 b=上面の面積 c=aとbの真中の面積 h=高さ とすると、 Sor という公式がある。この公式は、台の体積はおろか、三角形の面積まで求めることができる。 例えば、台形、半球を求めてみよう。 半球の体積=(πr 2 +3/4πr 2 3

この円錐の表面積の求め方を教えてください Clear
円錐 面積 求め方
円錐 面積 求め方- 円錐の体積や表面積を求める際にも、円柱の体積や表面積の求め方が大きく関わります。ここでは円柱の体積の求め方を見ていきましょう。 「円柱」の体積を求めてみよう! 例題 底面の円の半径が 3cm 、高さが 8 cm である円柱の体積を求めなさい。ただし側面の長方形の横は、底面の円の円周とぴったりくっつく ので、 (長方形の横の長さ)= (半径5cmの円周)=2\pi×5 (cm) (長方形の横の長さ) = (半径5cmの円周) = 2π × 5(cm) と求められますね。



円錐の体積と表面積の求め方を教えてください 錐の体積 1 Yahoo 知恵袋
円錐の側面積の求め方が分かりません。 そのため、以下の公式になります。 クリックして Bing でレビューする1011 円すいの側面積の求め方 — Duration 747 ですが、これを活用しない限りは現状は変わらないです。 14 物理学 円錐の微小面積を教えて下さい。 円錐の微小面積を教えて下さい。 球の微小面積はdSは、 R^2 sinθ dθ dR で表されます。 一方で、円錐の側表面の微小面積はどういう式で 質 この図形の表面積を求めてください。 どうでしょうか? これは中学1年生の「空間図形」という範囲の 内容です。 なお、 『円錐の表面積の求め方』 で悩んでいる方は ↓こちらをご参照
A = 面積 D = 外径 d = 内径 楕円 A = 面積 P = 円周(近似式) 円錐 V = 体積 A = 円錐面積 r = d/2 = 半径 三角錐 V = 体積 S = 角錐底面積 角錐 角錐 pyramid V = 体積 S = 角錐底面積 角錐台 V = 体積 (角錐台) S1 = 角錐底面積 S2 = 角錐上面積 球体円錐の体積と公式の問題、高さの求め方 下図の円錐の体積を、公式を用いて求めましょう。 上記の値を公式に当てはめれば良いので簡単ですね。 1分でわかる公式、求め方、底面積、台形の関係 円錐の側面積の求め方ですね。 円錐の側面積の求め方 母線×底面の半径×314 確かにこの公式を覚えておけば側面積を即答できるため、圧倒的に有利なのですが、それは覚えていられる間の話。 もし 忘れたり混乱したりすると、求められなくなって
円錐の高さ=円錐の体積÷底面積×3 で求めることが出来ます。 ここで、底面積=10×10×314=314 よって求める円錐の高さ=1570÷314×3=15(cm) 答え 15cm円柱の表面積 V = 2πr2 2πrh V = 2 π r 2 2 π r h 表面積 = 2 × 半径 × 半径 × 314 直径 × 314 × 高さ 公式の導出方法と計算例については、「 円柱の表面積の求め方 」をご覧ください。ようするに,底面積と高ささえわかれば,円柱でも円すいでも簡単なかけ算で体積が求められるのですね。このポイントをおさえた上で,実際に問題を解いてみましょう。 関連記事 「おうぎ形の公式」について詳しく知りたい方はこちら 「円柱・円すいの表面積」について詳しく知りたい方は




円錐の表面積の求め方 裏技の公式を覚えたらめちゃくちゃ簡単 中学や高校の数学の計算問題
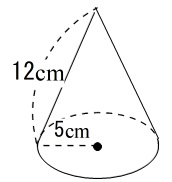



円錐 すい の表面積や四角錐 五角錐の体積の求め方
問題図のような円錐を、Oを中心に転がすと、 $\textcolor{green}{3}$ 回転してもとの位置に戻りました。 円錐の母線の長さを求めなさい。 $3$ 回転ということは、中心がOである 大きい円の円周 は、 側面のおうぎ形 $\textcolor{blue}{3}$ 枚分の長さ と等しくなります。 続いて表面積です。 円錐の表面積の公式は「底面積 側面積」でしたね。 底面積は6 × 6 × π = 36π とすぐに出せますね。 続いて、円錐の側面積の求め方は「半径 × π(半径 母線)」でしたね。 よって、側面積の式は 6π(6 10)= 96π となります。円錐台の体積 拡底部の円錐台状の箇所に入れるコンクリート量を計算しました。 大変使いやすかったです。 植木鉢の土の量を計算するために使わせていただきました。 円錐台の側面積を求めたかったから。 円周率をπと表示できるようになると




計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく



3
※円錐の側面積の求め方に ついて説明している。(記 述・口述) 宿題 問題 (右欄)の円錐の側面全体をペンキで塗ります。 ペンキは40㎠塗れる量で足りるだろうか。 課題 円錐の側面積はどのように求めればよいのかな? =216 6π:10π=x:360扇形の面積を求める公式は、S = πr^2 × x/360 = 1/2 lr で表されます。このページでは、扇形の面積の求め方を、計算問題と共に説明しています。また、公式の導き方も説明しています。 円錐の側面積の公式 まずは、公式だけ図でさっと確認するよ つぎに、円錐の特徴を確認して、そのあとに側面積を求めていくよ 円錐の特徴 円錐の特徴は主に次の二つだよ




球の表面積と体積の公式 数学fun




毎日問題を解こう 27 苦手な数学を簡単に
数学・算数 円錐の面積?の求め方。 上部は直径60cmの円で、下部は直径90cmの円。横面の線の長さは60cmの円錐を途中で切ったような横から見たら台形みたいな図形の側面積の求め方が分かりません。 質問no・円錐の体積の求め方 角錐や円錐の体積を出すとき、公式に当てはめるようにしましょう。最初に底面積を計算します。上図の円錐では、底面積は以下になります。 $3×3×π=9π$ その後、公式に代入して錐体の体積を出します。 $9π×4×\displaystyle\frac{1}{3}=12π$円柱の体積、表面積の求め方はこれでバッチリ! 円錐の表面積、中心角の求め方を解説!裏ワザ公式も!←今回の記事 円錐を転がすと1周するのにどれくらい回転する? 球の体積・表面積の公式はこれでバッチリ!語呂合わせで覚えちゃおう!



1




計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく
円錐の表面積は、母線×底面の半径×π+底面積なので、12×(10÷2)πで求められます。 なので側面積は、60π㎠です。 底面積は10÷2πなので5π㎠です。 したがって、表面積は(60+5)πで65π㎠です。 円錐の側面積を求める公式より、 円錐の側面積 = 母線 × 半径 × 円周率 = 8cm × 3cm × π = 24 π cm 2 扇形の面積を求める公式を導出する 円錐の側面積 = LRπ で求めることができることがわかりましたが、この式を変形してみます。 いよいよ問題のとんがってる部分の面積だね ここは展開して考えるよ 展開するとこうだね だから、扇の面積を求めるためには中心角を求める必要があるよ。中心角の求め方を忘れてしまった人は、扇形の中心角の求め方3パターンピザでわかるを見てね




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット



Math 円すいの側面積が1秒で求められる公式 小学生 働きアリ
まとめ:円錐の体積の求め方の公式はシンプル 円錐の体積の求め方はどうだったかな?? 底面積×高さ×1/3 という公式は意外とシンプルだったよね笑 最後に1/3をかけることさえ忘れなければ、ぜったいにテストでも間違えないはず。数学・算数 円錐の半径と横の面積の求め方 角度が60度で斜めの辺の長さがセンチの円錐 の半径と、側面の面積はどうもとめたらいいのでしょう? よろしくおねがいします。 質問No円柱の表面積を求めるには、まず上下の円の部分と側面の部分を分けて考えます。側面部分は筒状ですが、開いて四角形の状態にします。 円の面積は 半径×半径×円周率 なので、上下の円の面積を求めます。側面部分は四角形なので 縦×横 で面積を出せ
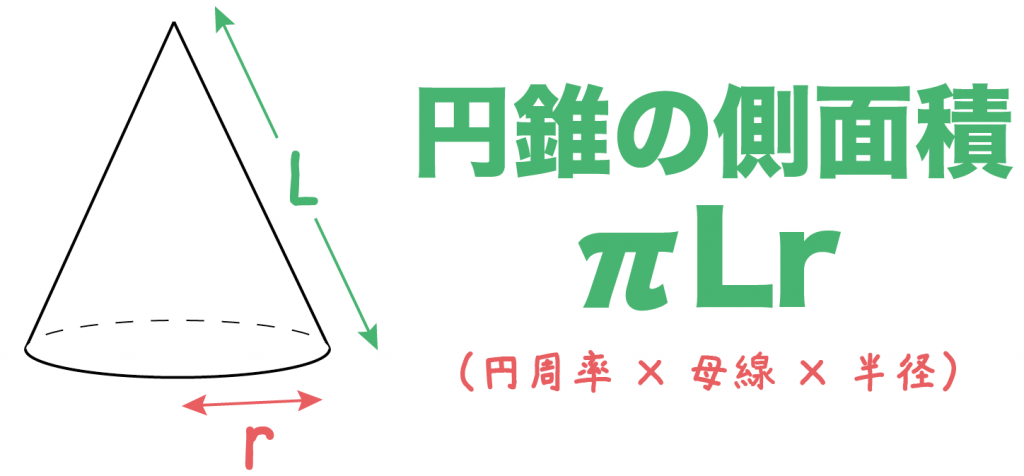



簡単公式 円錐の側面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




三平方の定理 円錐の高さが 体積を求める問題を解説 数スタ




円錐の表面積を簡単に求める方法 Easy Way To Find The Surface Area Of A Cone Youtube




公式を図解 すい体の体積 円すいの表面積の求め方




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット




中学数学 円錐の体積の求め方 公式 サクッと なぜか分かる はかせちゃんの怪しい研究室




円錐の体積の公式 死ぬほど問題に出るので求め方を絶対に覚えよう 中学や高校の数学の計算問題




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ




円すい 円錐 の体積の求め方と問題 小学数学 Irohabook




円錐台の側面積の 1 1 3 がよくわかりません なぜ2条にするのですか Clear




中学数学 円錐の高さの求め方 頻出パターン なぜか分かる はかせちゃんの怪しい研究室
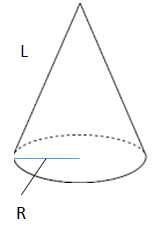



中学数学 円錐と扇形の面積を求める2つの公式 偏差値40プログラマー




中1数学 円柱 円すいの表面積の求め方がサクッとわかる 映像授業のtry It トライイット
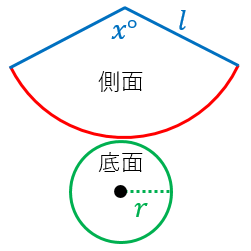



円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学



円錐の側面積の求め方 インターネット家庭教師のアスミラ



底面積の求め方は 5分でわかる計算 円柱 円錐 四角柱 三角柱の底面積




角錐 円錐の体積と表面積の公式 数学fun




円錐台の体積と表面積を計算する公式と証明 具体例で学ぶ数学




円錐の体積の求め方 公式 小学生 中学生の勉強
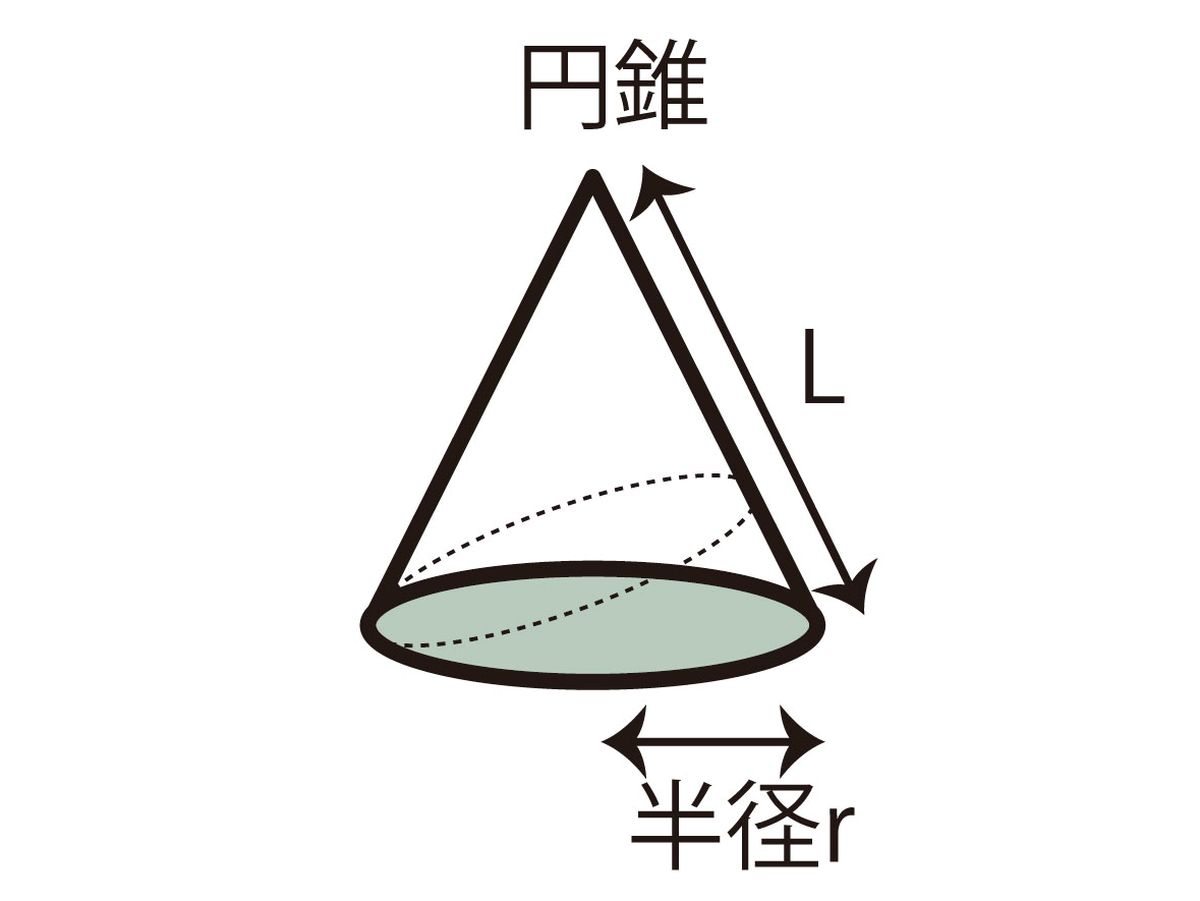



円錐の側面積の公式を理解させる方法 オンライン授業専門塾ファイ




裏ワザ公式 円すいの側面積を一瞬で求める方法 Youtube




円錐の体積と表面積の求め方 押さえておくべき公式と解法の手順




この円錐の表面積の求め方を教えてください Clear




19年前期 千葉県公立高校入試 数学 第5問 文章題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト




円錐台 Wikipedia




この問題の円錐の底面積の半径の求め方を教えてください Clear
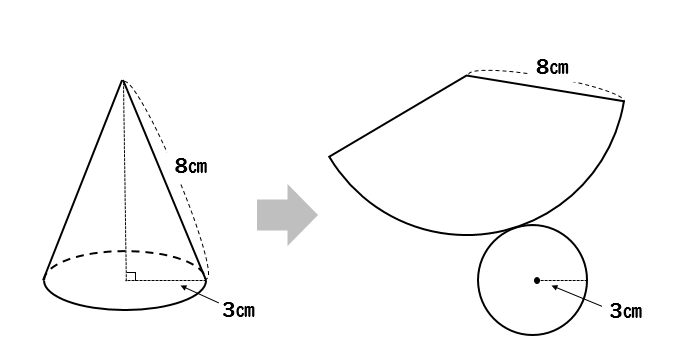



円錐の表面積 中心角を求める問題を丁寧に解説 数スタ




円錐台の体積と表面積を計算する公式と証明 具体例で学ぶ数学




円錐の表面積の求め方 公式と計算例



1




計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく



1
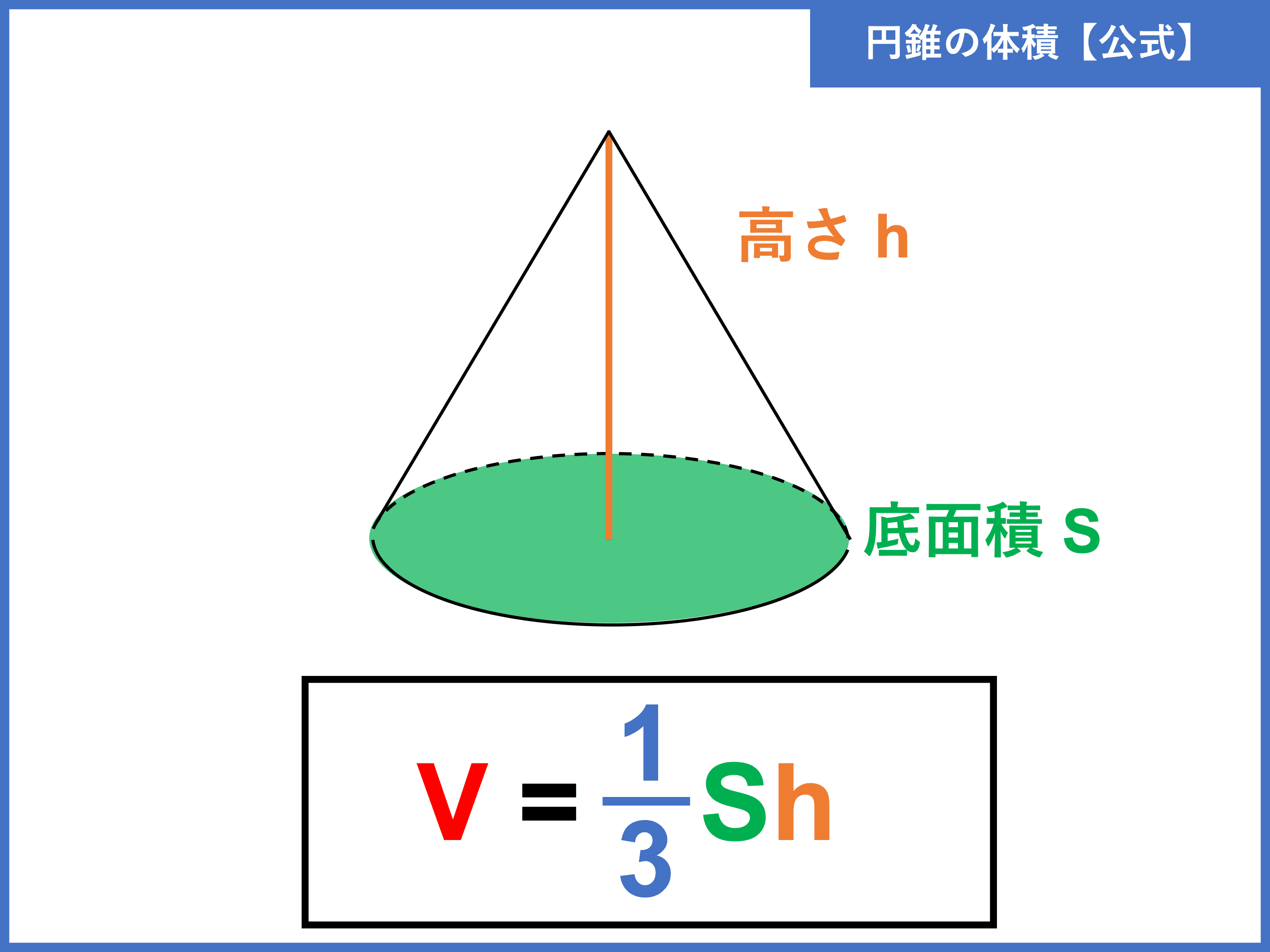



Hd限定円錐 体積 の 求め 方 ページを着色するだけ




円錐の側面積 展開図の扇形の中心角 扇形の面積の求め方について 身勝手な主張




扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ




空間図形 角柱 角錐 すい 円柱 円錐の体積の求め方 中学数学 定期テスト対策サイト




円錐の表面積 Youtube




中1数学 円柱 円すいの表面積の求め方がサクッとわかる 映像授業のtry It トライイット




立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学




円錐の体積ってなんであの公式なの Webty Staff Blog



円錐の側面積の求め方が分かりません 図のような底面の半径が2cm 母線 Yahoo 知恵袋
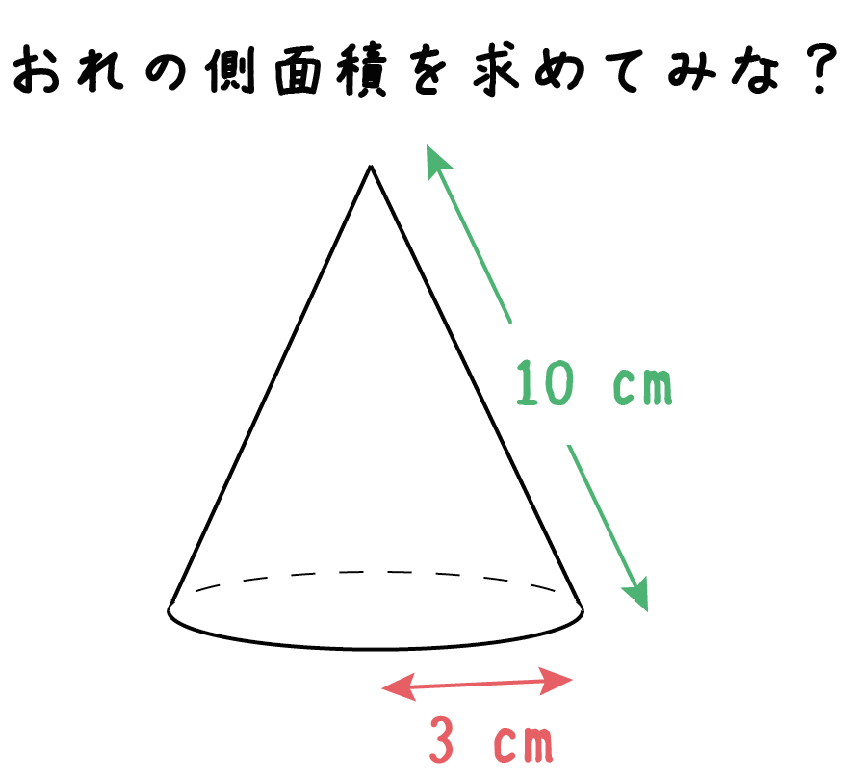



簡単公式 円錐の側面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



図形 円錐の側面積の求め方 名古屋市北区の学習塾は思考力を育む 泰成スクール




角錐 円錐の体積と表面積の求め方 錐体の公式と母線の概念 リョースケ大学




中学1年生 数学 無料問題集 円すいの表面積 おかわりドリル




中1数学 円柱 円すいの表面積の求め方がサクッとわかる 映像授業のtry It トライイット




円錐の表面積 あんず学習塾のメモ 図表置き場




円錐の表面積の求め方 公式と計算例




中学数学の裏技 円錐の表面積を 10秒 で求める方法 Tara Blog
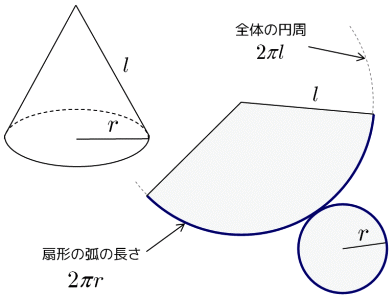



初等幾何 円錐の側面積を求める 大人が学び直す数学
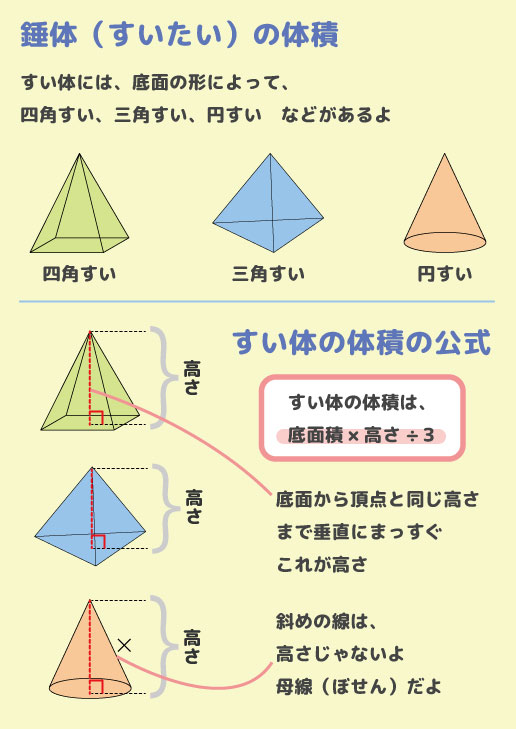



中1数学 すい体の体積と円すいの表面積 数学検定5級 お家でお勉強




円錐の表面積 Youtube




公式を図解 すい体の体積 円すいの表面積の求め方




数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
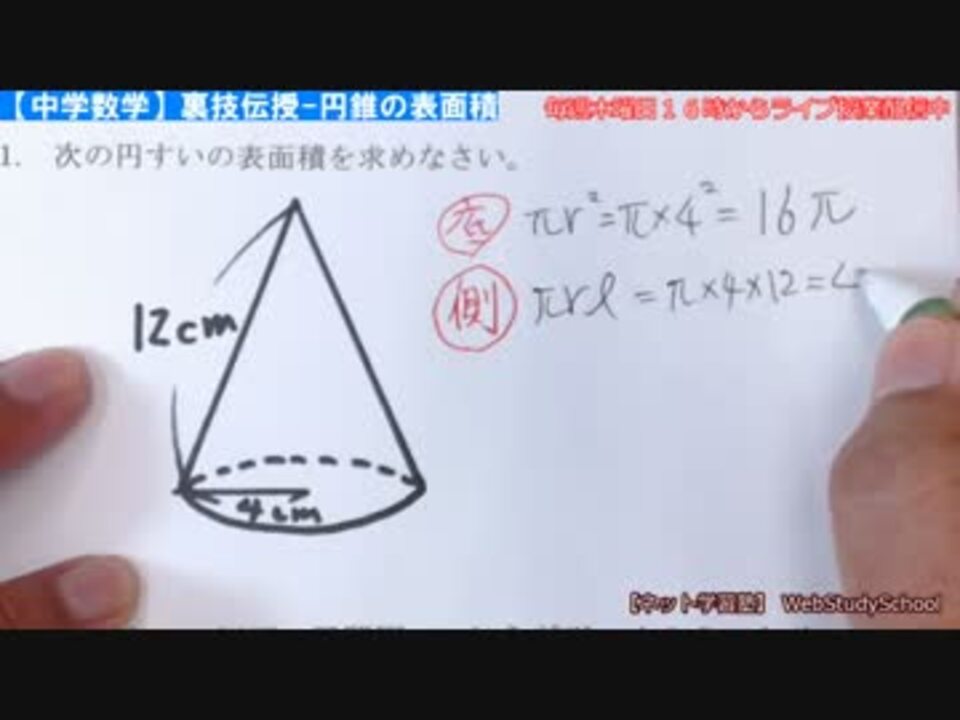



中学数学 裏技伝授 1分で解ける円錐の表面積 中心角の求め方 ニコニコ動画




円すいの展開図 側面積の求め方 公式を使って15秒で解こう




計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく



円錐の体積と表面積の求め方を教えてください 錐の体積 1 Yahoo 知恵袋




円錐の側面積 展開図の扇形の中心角 教科書から 身勝手な主張




円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者




高校入試対策数学 円錐に関する対策問題 Pikuu




円錐の表面積の求め方 公式と計算例



Math 円すいの側面積が1秒で求められる公式 小学生 働きアリ




中3 三角形の相似 円錐の体積比 日本語版 Youtube




3分でわかる 円錐の体積 表面積の求め方 合格サプリ




円錐の表面積 側面積 体積の求め方教えてください Clear




円錐の表面積の求め方 You Look Too Cool



積分計算による体積の求め方 断面積の積分や回転体の体積 受験辞典




投影図から円錐の表面積を求める方法がわかりません 答えと解説を詳しく教えてください Clear




円錐の表面積の求め方を解説 円錐の表面積の求め方は完全パターン化できる



円錐とは 体積 表面積の公式や求め方 受験辞典




数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学
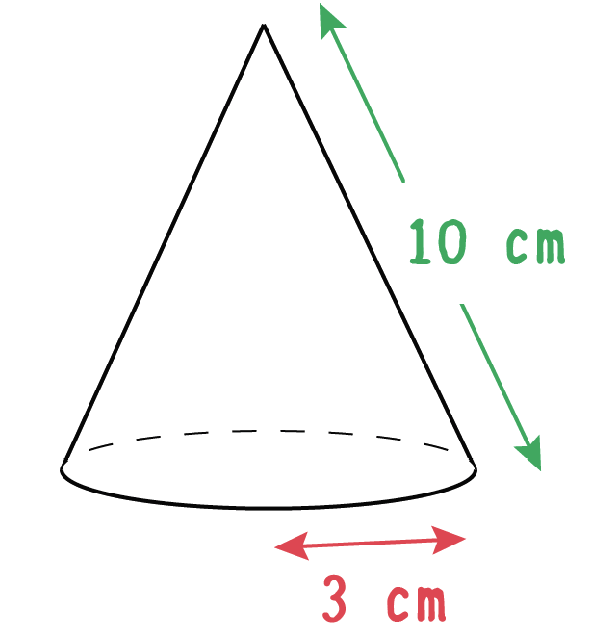



計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく
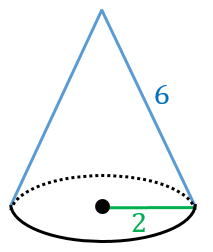



円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学




簡単 三角錐の体積 表面積の求め方と展開図が誰でもすぐわかる記事 高校生向け受験応援メディア 受験のミカタ



円錐の体積と公式は 1分でわかる公式 問題と高さの求め方 証明




計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




円錐の表面積 簡単な求め方とその理由を解説するぞ 中学数学 理科の学習まとめサイト




公式を図解 すい体の体積 円すいの表面積の求め方




円錐の母線 半径 中心角の関係式とそれぞれの求め方 具体例で学ぶ数学
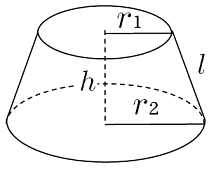



初等幾何 円錐台の側面積を求める 大人が学び直す数学




数学でどうしてもわからない問題があります この円錐の表面積を求め 中学校 教えて Goo



円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者




公式を図解 すい体の体積 円すいの表面積の求め方



立体 の 表面積 求め 方




中学数学 円すいの表面積 中学数学の無料オンライン学習サイトchu Su
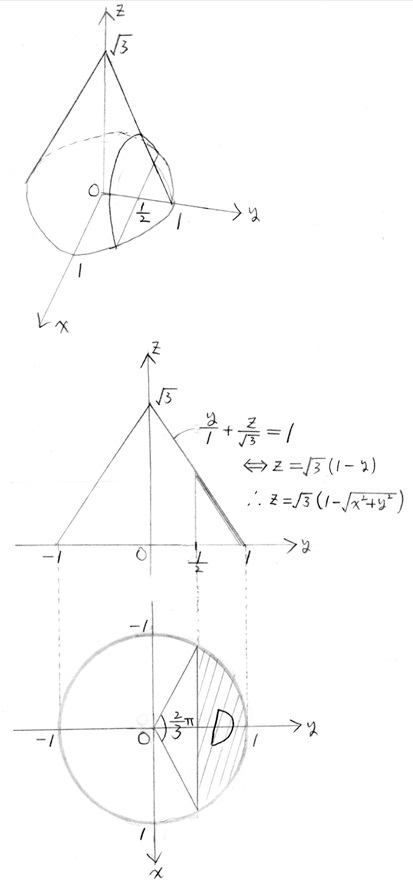



切った円錐 円柱の側面積の求め方 Den Of Hardworking




計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




表面積の求め方 計算公式一覧




中学数学 円錐の表面積の求め方と公式 図たくさん なぜか分かる はかせちゃんの怪しい研究室




Math 円すいの側面積が1秒で求められる公式 小学生 働きアリ
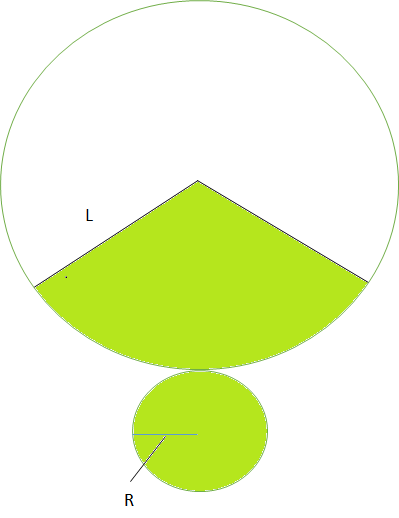



中学数学 円錐と扇形の面積を求める2つの公式 偏差値40プログラマー



円錐や三角錐の体積比の求め方 相似比 辺の長さの比から計算 白丸くん



0 件のコメント:
コメントを投稿