1800 · 余弦定理で角度を求める方法 数学の星 だよ これを覚えておけば 三平方の定理を使わなくて辺の長さを計算できちゃうんだ 楽に解けるんなら知っておきたいよね んでそのパターンは全部でつぎの3つ 3060の直角三角形 Pythagorean theorem は直角三角象限の法則law of quadrants (1) 直 角 球面三角形において,直角以外の角とその 対辺 は同じ 象限 にある. (2) 直角球面三角形において,2 辺 が同じ象限にあれば,残りの辺は第一象限にある.もし2辺が異なる象限にあれば,残りの辺は第二象限にある.三平方の定理 (さんへいほうのていり)、 勾股弦の定理 (こうこげんのていり)とも呼ばれる。 三平方の定理によって、直角三角形をなす3辺の内、2辺の長さを知ることができれば、残りの1辺の長さを知ることができる。

中学数学 三平方の定理 直角二等辺三角形 オンライン無料塾 ターンナップ Youtube
ディスプレイ 三角形 の 法則
ディスプレイ 三角形 の 法則- · まさよさんの「エネルギーの魔法」のp74~p75に、三角形の法則についての説明があります。 これは、まさよさんのエネルギーの流し方の基本です。 F様との間で、三角形の法則で遠隔でエネルギーを流す実験をしてみました。三角形には不思議な性質がたくさんあります。 その中にはまだ発見されていないものもあるはずです。 このジオジェブラを使うと正確な作図が簡単にでき、さらにアニメーションを使って変化を調べることができ、新しい発見が容易にできます。 「bもしかしたら・・・?




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット
動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru1103 · この記事では、「直角三角形」の定義や合同条件、重要な辺の長さの比について解説していきます。 また証明問題もわかりやすく説明していくので、ぜひマスターしてくださいね! 目次直角三角形の定義直角三角形の定理(三平方の定理この三角形に並べられた数字には、次のような法則があるのがわかります。 「ある数は、その1つ上の行の隣接する左右の数の和によって求まる」 例えば、上図の赤い部分では、 6+4=10 となっていま
· しかも 個以上の三角形を見つけられれば、IQ1以上確実! ということで、この問題は多くのTwitter民たちのクイズ心に火を点けたもよう。ネット上には様々な回答が寄せられている。 あなたはいくつの三角形が隠れているか分かるだろうか?1210 · 三角形の法則なら1分でディスプレイが完成する "三角形の法則なら1分でディスプレイが完成する" 著書『 今あるもので「あか抜けた」部屋になる。 』 お部屋づくりののルールを紹介していまして、その中の1つです。 先日出演したNHK 「あさイチ」でもお話しました。 この赤い三角形はスタッフさんの手作り! 石井アナとソーシャルディスタンスがパスカルの三角形のもっとも簡単な応用は 二項展開 です.これはつぎの 二項定理 に基づいています. 二項定理: (x y)n = n ∑ k=0nCkxkyn−k ( x y) n = ∑ k = 0 n n C k x k y n − k これより, (xy)n ( x y) n を展開したときの各項の係数は,二項係数になります
(三角形の角の二等分線に関する公式) (証明) CからADに平行な直線を引き、BAの延長線との交点をEとする。 よって、 ACEは二等辺三角形、AE=AC。 ADとECが平行より、AB:AE=BD:DC、三角形定则 是平面力系求解力的合成与分解的基本法则 1 有两个成α(0内接円といい、中心を内心といいます。 下の「定理8」は三角形の3つの角の二等分線は1点で交わること の証明ですが、その証明方法をはじめてみる方にとっては、「へぇ~ 垂線か」と思われるかもしれませんが、「角の二等分線」が「各辺から の距離




必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ



数学のコツ 三平方の定理 個別指導ソラオトのスタッフブログ
· ってことは、この三角形は3 4 5の直角三角形ってことがわかるね。 bc ab = 3 5 になってるはずだから、 abはbcの3分の5倍だね。 よって、 ab = bc× (3分の5) = 10 cm になるね。 3 4 5の直角三角形の比もよく出てくるからしっかり押さえておいてね。1718 · 逆三角形の法則 そう、お客さんにプレゼンするには この順番、法則がすごく大事です。 今日の話は、会社のコンセプトを 決めるのと同じくらい 重要な内容ですので、 ぜひ時間を作って考えてみてくださいね。 それでは今日は この辺で失礼致します。S formula (1) area S = √s(s−a)(s−b)(s−c) s= (abc) 2 T r i a n g l e b y H e r o n ′ s f o r m u l a ( 1) a r e a S = s ( s − a) ( s − b) ( s − c) s = ( a b c) 2 お客様の声 アンケート投稿 よくある質問




中学受験算数 等積変形の利用 ヒポクラテスの月




正弦定理から 三角形の辺の長さを求める計算について 数学 苦手解決q A 進研ゼミ高校講座
桃 == 《三平方の定理》 == → 印刷用PDF版は別頁 《解説》 次のような直角三角形の3辺の長さについては, a 2 b 2 =c 2 が成り立ちます.(これを 三平方の定理 といいます.) これを用いて3辺の長さのうち2辺の長さが分かっているとき,残りの1辺の長さを求めることができます. 証明 ・・・ 証明の仕方は何十通り~何百通りあると言われています。 中でも · って聴いたことありますか? 私は、その法則の存在を知ってはいましたが、それを論理的に説明されたのは初めてでした!! ↓↓↓ 恋愛三角形の法則とは 直角三角形を イメージしてください。 左下の角が自分 左上が進化した自分 右下が運命のお愛手 とします。三角形を書くための条件(中学2年生程度) 三角形を書けと言われたときに、次の3つの条件のうちどれかが与えられれば三角形を書くことが出来ます。 1 三つの辺がの長さが与えられた時 2 二つの角の大きさとその間の辺の長さが与えられた時 3 二つの辺の長さとその間の角の大きさが与えられた時 それでは実際に書いてみます。




ヘロンの公式とは 図解でわかるその仕組みと証明方法 アタリマエ




無料ダウンロード三角形 の 法則 最高のぬりえ
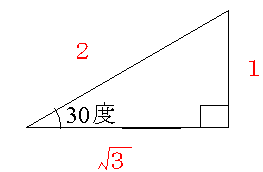
· 会話中の気まずい雰囲気は「三角形の法則」で目線を変えてみる 相手に良い印象を与えるのにアイコンタクトは不可欠ですが、やりすぎは逆効果です。 相手の目を見すぎると、気分が悪くなる人もいるのです。 米国のニュースサイト「The Daily Muse」によると、気まずくならない印象的なアイコンタクトをするには、視線を三角形沿ってに動かすと良いそう(abc) 4 の三角形の12ab 2 cを例に説明します。 (abc) 3 の三角形において、(abc) 4 の三角形の12ab 2 cと同じ位置にあたるのは6abcです。 また、6abcの上に位置するのは3ab 2 、3b 2 cです。 それぞれの項の文字だけをみると、(abc) 3 の三角形のabc,ab 2,b 2 cは(abc) 4 の三角形のab 2 cをそれぞれb,c,aで割った直角三角形においては三平方の定理が成り立つため,3つの角が30°,60°,90°である直角三角形と,45°,45°,90°である直角三角形の3辺の長さには,それぞれ次のような関係が成り立っています。 特別な直角三角形の3辺の比 30°,60°,90°の 直角三角形 45°,45°,90°の 直角三角形 3辺の比は となります。 3辺の比は
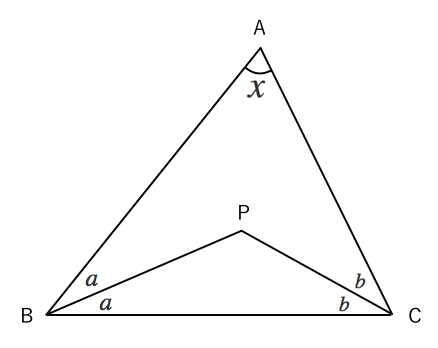



図形の調べ方 三角形 役に立つ角度の求め方 苦手な数学を簡単に




三平方の定理 特別な直角三角形の3辺の比 中学生からの質問 数学 進研ゼミ中学講座 中ゼミ
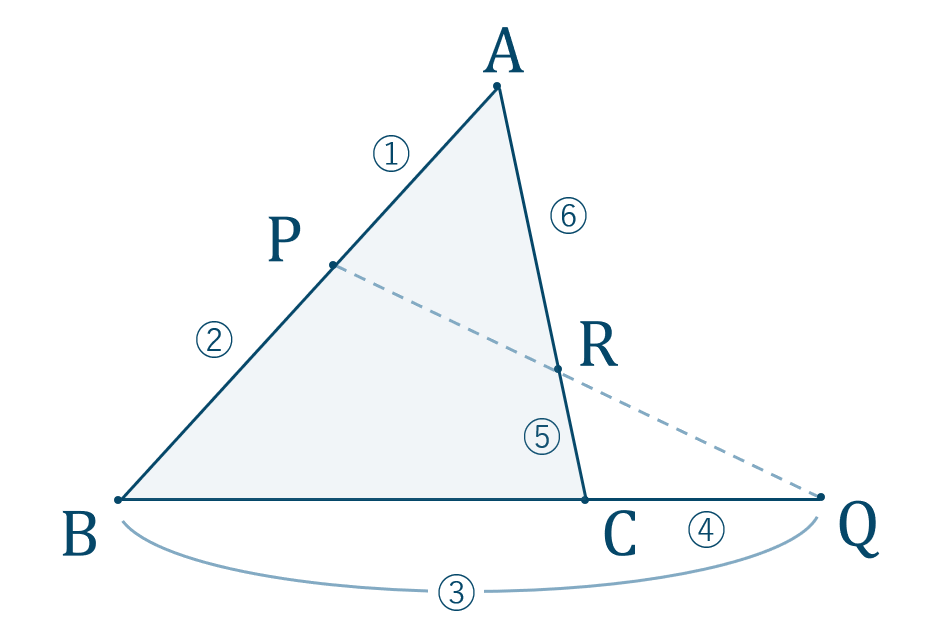
弧ABに対する円周角の大きさはつねに一定であり、その角の大きさは、その弧に対する中心角の大きさの半分である。 ・∠ACB=∠ADB ・∠AOB=2∠ACB=2∠ADB また、次の図のように2つの円周角があったとき ・∠AEB=∠CFDであれば、その円周角に対する弧(ABとCD)の長さは等しい ・弧ABと弧CDの長さが等しければ、その弧に対する円周角の大きさは等しい(∠AEB=∠CFD)チェバの定理・メネラウスの定理 チェバの定理・メネラウスの定理 三角形ABCの辺BC,CA,AB上に点D,E,Fをとり、線分AD,BE,CFが1点Gで交わるとき、以下の等式が成り立つ。 チェバの定理の証明 図のように、a= BCG、b= CAG、c= ABGとします。 AF/BF=b/a、BD/CD=c/b、CE/AE=a/c より、 (AF/BF)(BD/CD)(CE/AE)=(b/a)(c/b)(a/c)=1 メネラウスの定理の証明 · 解説:三角形面積2等分の法則 三角形を2等分する有名な公式があります: 上図のようにADDC=p1p及びAEEB=q1qと内分した時、 であれば緑の直線は三角形の面積を2等分します(この理由は後述で深堀します)。この法則を設問に照らし合わせてみましょう。




三角形の比 角の二等分線の定理 性質の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生
パスカルの三角形 日本では、高校1年生もしくは2年生で、次のような三角形に出会う。 この三角形は、パスカルの三角形といわれているが、ブレーズ・パスカル(1623 1662) が現れるはるか以前からパスカルの三角形については研究されていたという。 · 連続する二等辺三角形の角度の法則() 重なり部分の面積を考える(麻布中学 13年)() 30゜、60゜、90゜の三角形の面積を求める方法() 二等辺三角形を見つける(共立女子第二中学 10年 )() 「 · 三角形の底辺に平行な線を1本引けば分かります。 黄色と青色のマルは、錯角同士で同じ大きさになるからですね。 他にもいくつか証明法を知ってますが、気になる方はググって下さい。



中学数学 三角形と比




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット
三角形の内角の性質 三角形の内側にある角のことを 内角 といい、 すべて足すと180° になります。 これは小学生のときに学習しているので覚えている方も多いでしょう。 でも じゃぁ、何で180°になるのか知っていますか? と言ったら、困ってしまいこれらの関係をまとめると、以下の球面三角形の正弦法則が得られる。 sina/sinA = sinb/sinB = sinc/sinC (1) 球面三角形の余弦法則 基準面上のOB'A'C'の関係は上図のようになる。 B'からOC'に垂線B'C''、そしてこの線にA'から垂線A'A''を引く。 すると、∠A'B'C''=aであるから、B'C''=coscsina、A'A''=sinccosBsinaとなり、 OC''=cosccosaとなる。 (∠A'B'C''=90°∠OB'C''=∠B'OC''=a) · パスカルの三角形の作り方、覚え方! 両端に1を書く 間に数を埋める。 完成! パスカルの三角形の使い道 練習問題に挑戦! まとめ 数学の成績が落ちてきたと焦っていませんか? こちらの関連記事はいかがでしょうか?
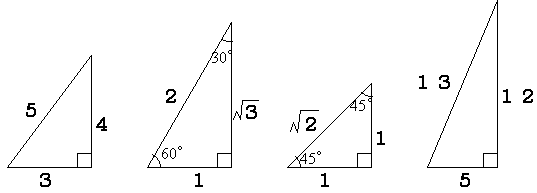



三角形の性質




高さがわからない二等辺三角形の面積の求め方 三平方の定理を使えばバッチリ 数スタ
04 · パスカルの三角形とは 本題に。 パスカルの三角形とは何なのか。 「 パスカルの三角形は、二項展開における係数を三角形状に並べたものである。 (Wikipedia)」 まったく分からんね。 要は、 これ。 パスカルの三角形の作り方 まず1を書く。 1




中学数学 三平方の定理 特別な直角三角形 中学数学の無料オンライン学習サイトchu Su




世界に一つだけの 三角形ペア 発見 慶大院生2人証明 朝日新聞デジタル




パスカルの三角形と二項定理による展開との関係とは 二項係数の性質を証明 遊ぶ数学




交流回路でよく使う三角形の比 電験三種講座の翔泳社アカデミー



質問にお答えします 小学生でもわかる数学とは 教育研究所arcs




メネラウスの定理が5分でわかる 証明や使い方をイラスト入りで詳しく解説



三平方の定理が一瞬で理解できる 公式 証明から計算問題まで解説 Studyplus スタディプラス




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ



三平方の定理



公式一覧と使い方 解き方 数学a 図形の性質 教科書より詳しい高校数学




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



三角比 三角関数の定義 相互法則や90 8の関係など 数学の偏差値を上げて合格を目指す



スリッパの法則 って 知っていますか ニッセイ基礎研究所



1
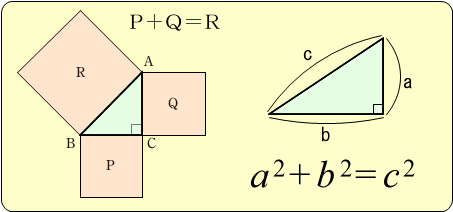



見えますか タイルの模様からピタゴラスの定理 Note Board
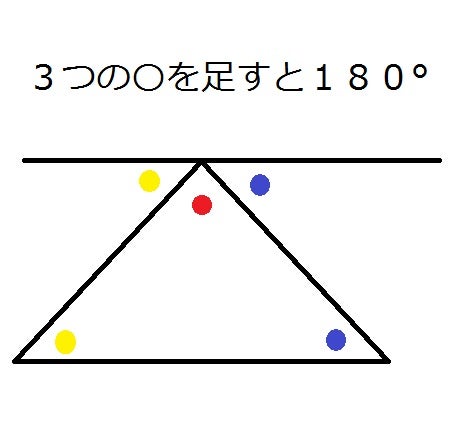



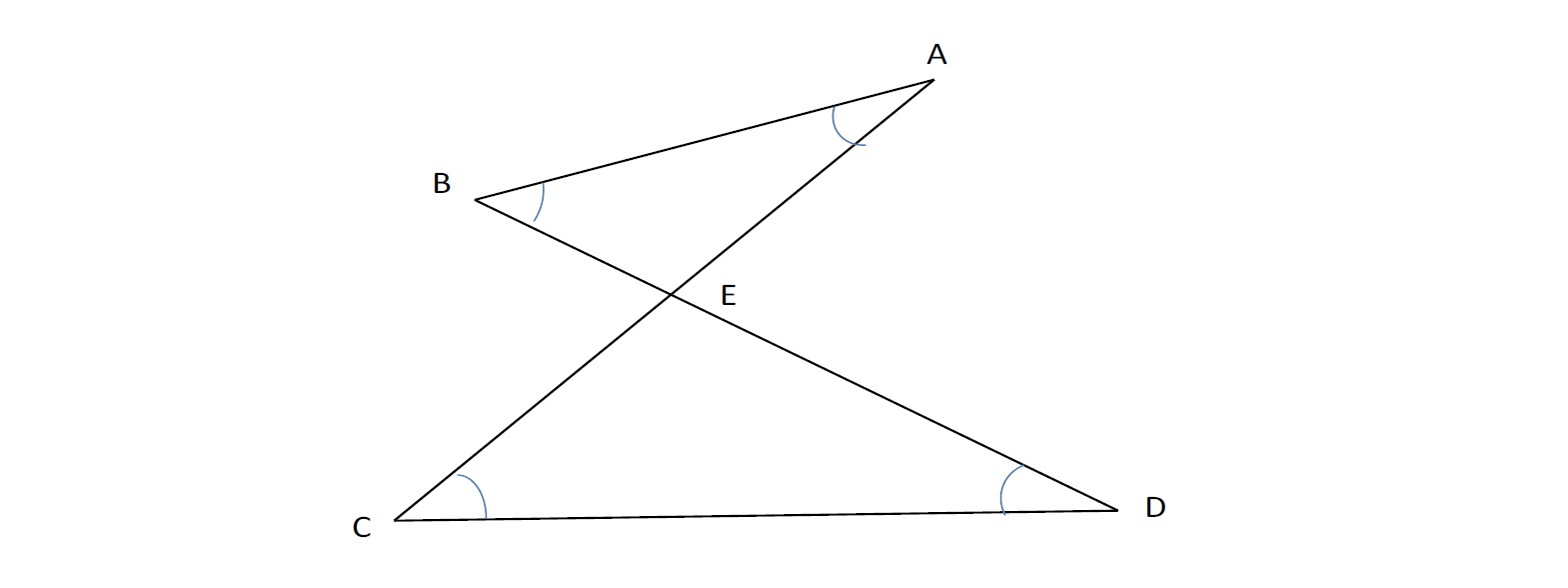
三角形の内角の和は なぜ180 になるのか スリッパの法則 ブーメランの法則 東大に文理両方で合格した男が綴る 受験の戦略



中学数学 三角形と比




中学数学 三平方の定理 直角二等辺三角形 オンライン無料塾 ターンナップ Youtube




高校数学 直角三角形を用いた三角比 Sin8 Cos8 Tan8 の定義とその理由 30 45 60 の三角比 受験の月
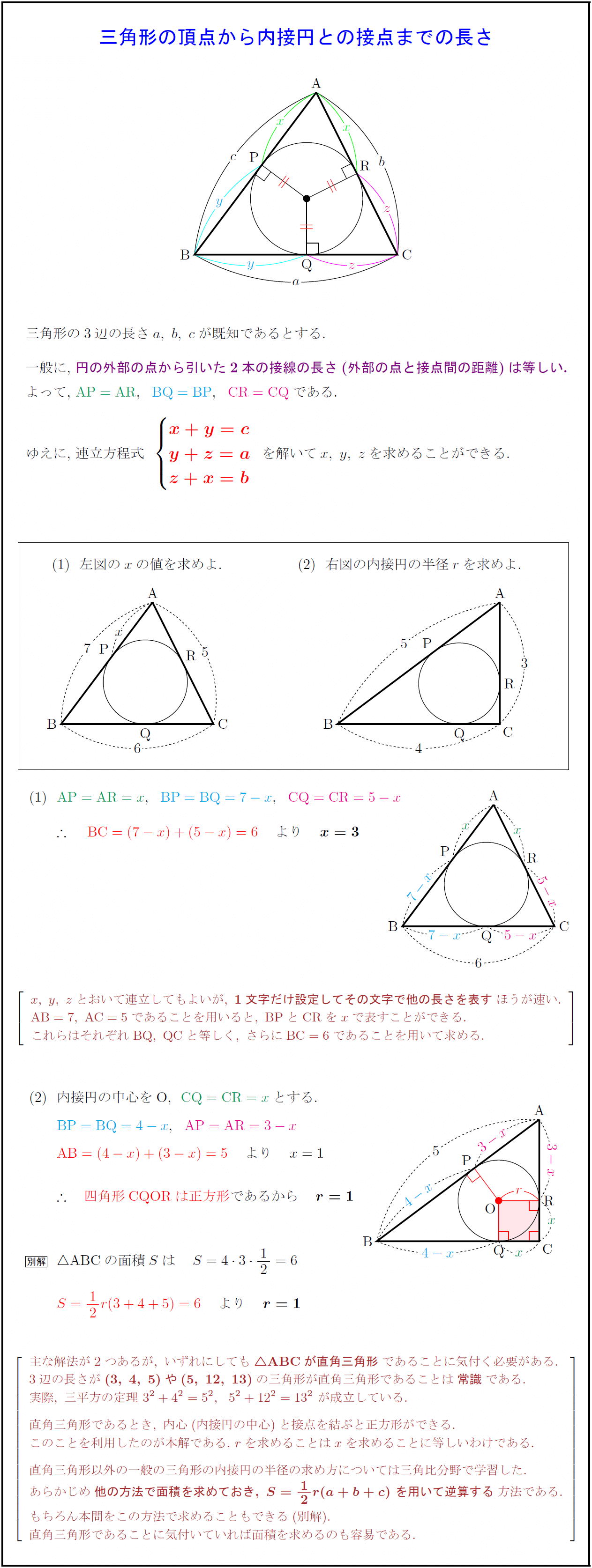



高校数学a 三角形の頂点から内接円との接点までの長さ 受験の月
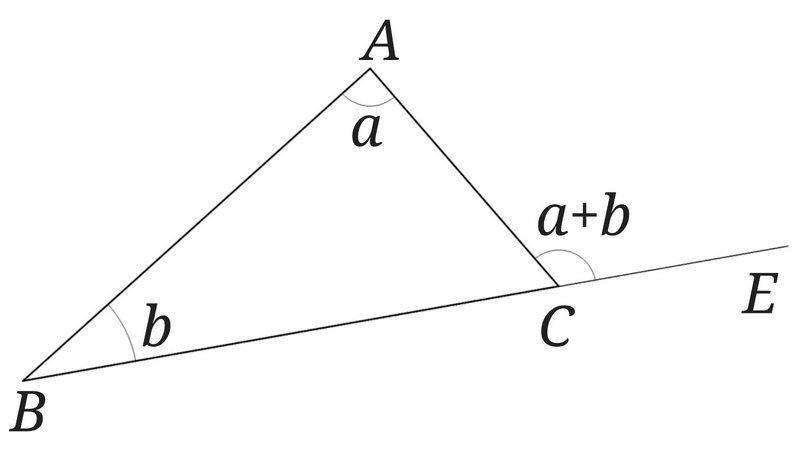



数学の図形で使えるスリッパの法則を使って星の角度の和をだそう まぜこぜ情報局




三角形の重心の性質とその証明 求め方 数学a By となりがトトロ マナペディア



Kistenkasten723 オームの三角形 日本では オームの法則の図は 円で描かれるが 英語圏やドイツ語圏では 三角形で表現され Ohm S Law Triangle と呼ばれる 掛算 超算数 算数 算数教育 オームの法則 みはじ図 くもわ図 きはじ T Co




三平方の定理 ピタゴラスの定理 とは 応用問題パターンまとめ10選 遊ぶ数学




三平方の定理 覚えること 辺の長さ 苦手な数学を簡単に



面積と辺の比の関係を解説 図形の面積と辺の比の関係はテントやドリルで面積を求める




簡単計算 二等辺三角形の高さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




三角形の成立条件とその証明 高校数学の美しい物語



プログラマーのための数学 三平方の定理 ピタゴラスの定理 Qiita



直角三角形とは 定義や定理 辺の長さの比 合同条件 受験辞典



三平方の定理が一瞬で理解できる 公式 証明から計算問題まで解説 Studyplus スタディプラス




三角比 30 45 60 もう一度やり直しの算数 数学
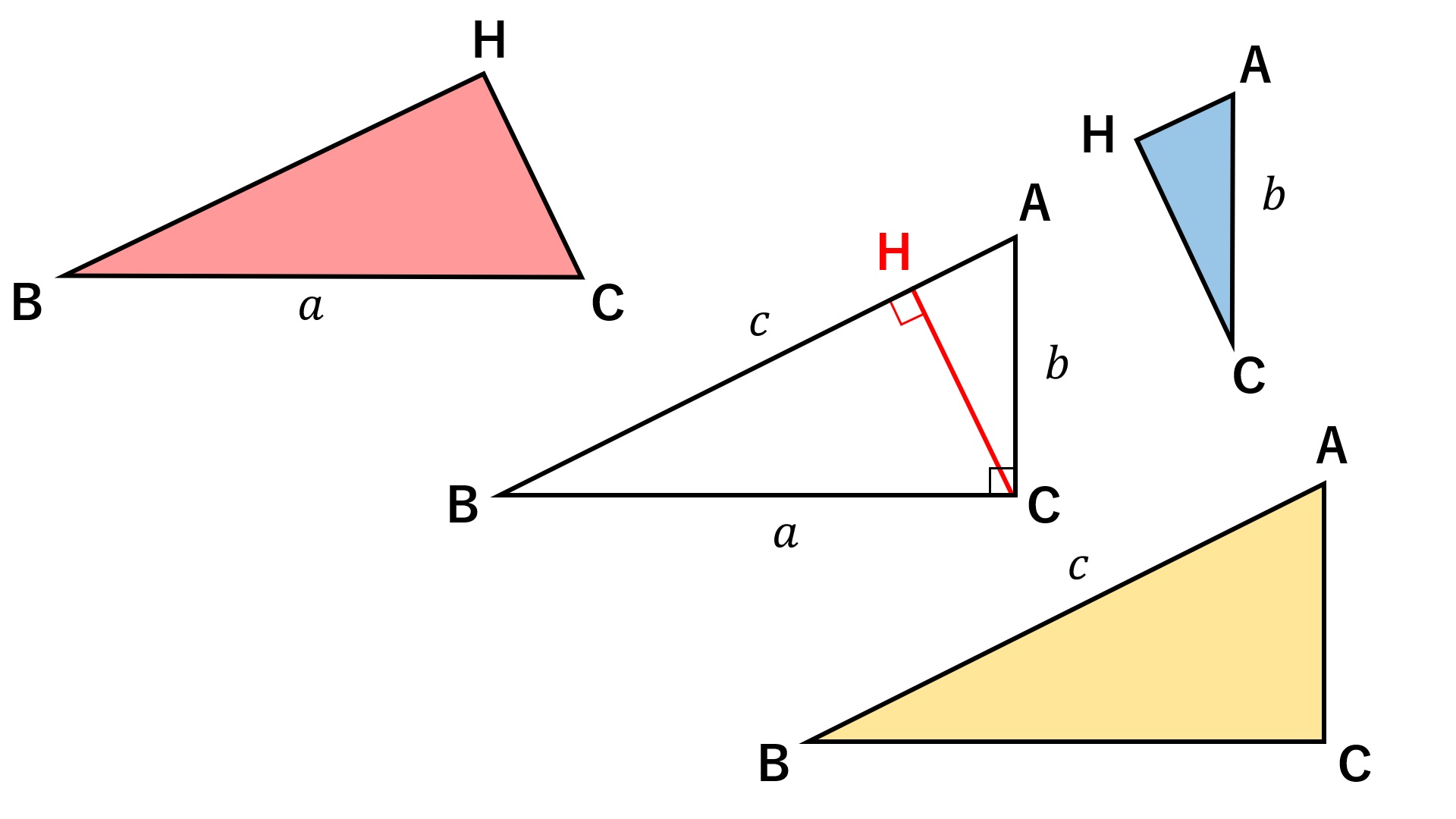



感銘を受けた数学 三平方の定理の美しき証明たち 数学 統計教室の和から株式会社




必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ




余弦定理で角度を求める方法 数学の星




鏡の法則の本質的な意味 鏡の法則は実は三角形だった 一家に一人のセラピストー戦場で働く男性を癒すパートナーシップ論ー ライフシフト総合研究所



三角形の内角30度 60度 90度のとき辺の比は1 2 Root3になる Yahoo 知恵袋
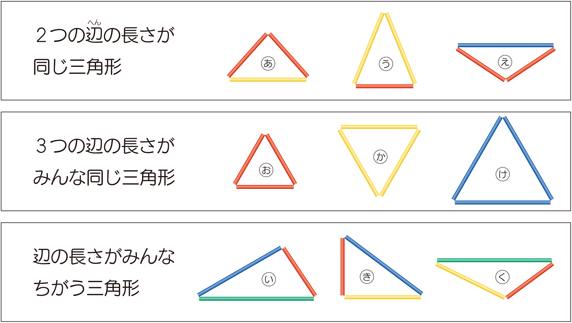



二等辺三角形と正三角形 算数用語集
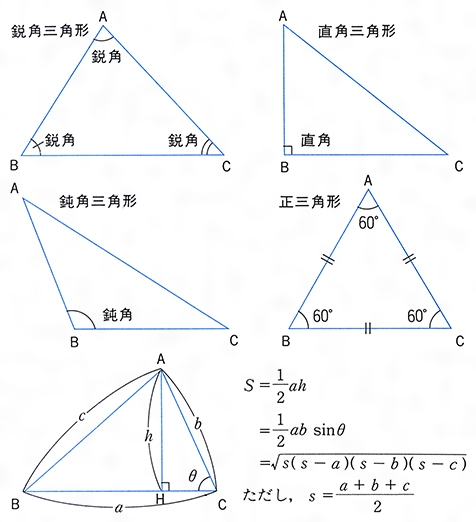



三角形とは コトバンク




Diy上達法 サシゴの法則とは クリエイティブライフ アトリエ1625




三平方の定理 特別な直角三角形の比を使った計算のやり方は Youtube




逆三角形の法則 Or The Rules Of The Inverted Triangle General Discussions Cardano Forum




感銘を受けた数学 三平方の定理の美しき証明たち 数学 統計教室の和から株式会社
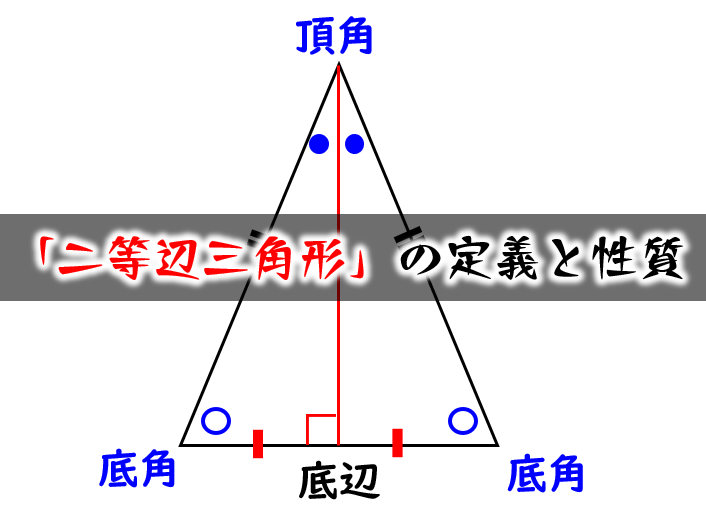



二等辺三角形の定義と性質 問題の解き方 数学fun




三角形の比 角の二等分線の定理 性質の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



七五三 三角形から円に内接する四角形へ




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



パスカルの三角形と最短経路 思考力を鍛える数学
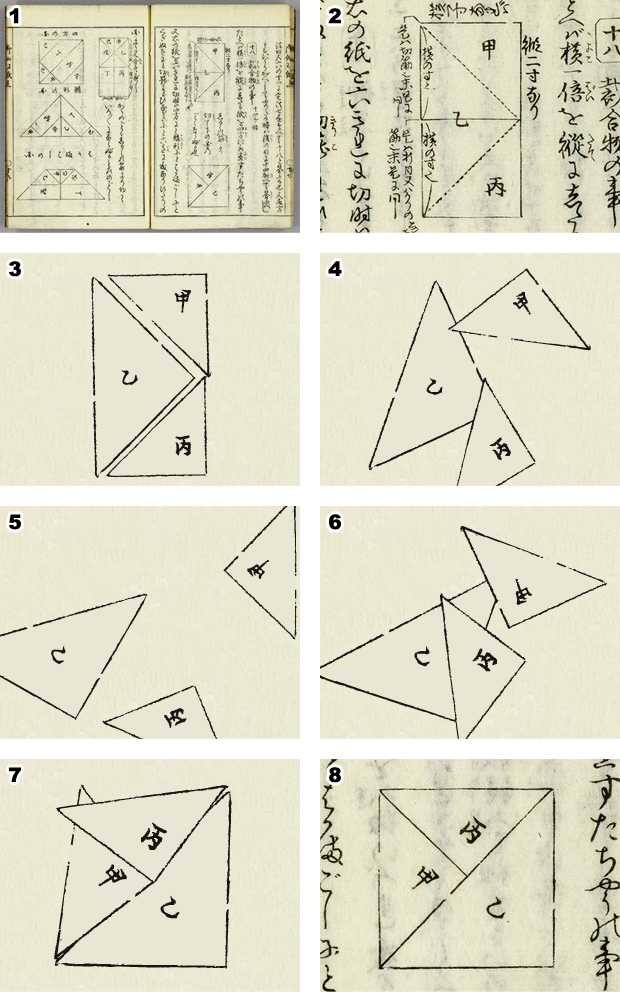



コラム ピタゴラスの定理 江戸の数学



パスカルの三角形と最短経路 思考力を鍛える数学




三角形の法則なら1分でディスプレイが完成する インテリアコーディネーター荒井詩万のブログ



三角形とは 面積公式 角度 辺の長さ 重心 比の計算 受験辞典




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット




逆三角形の法則でロジックを絞り込みましょう 地方自治体の宣伝や広報でお悩みの担当者さん 必見 宣伝の新しい形
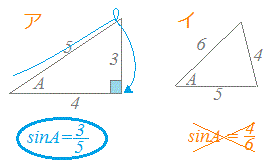



正弦定理




直角三角形 Wikipedia




三平方の定理と二等辺三角形 Youtube
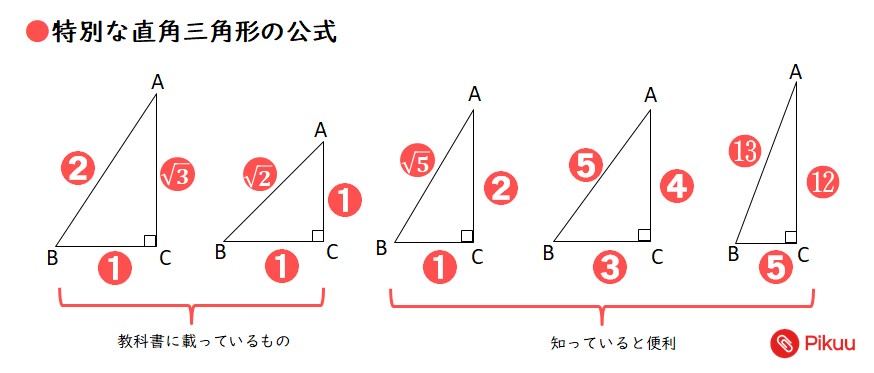



高校入試対策数学 特別な直角三角形を使った問題 Pikuu
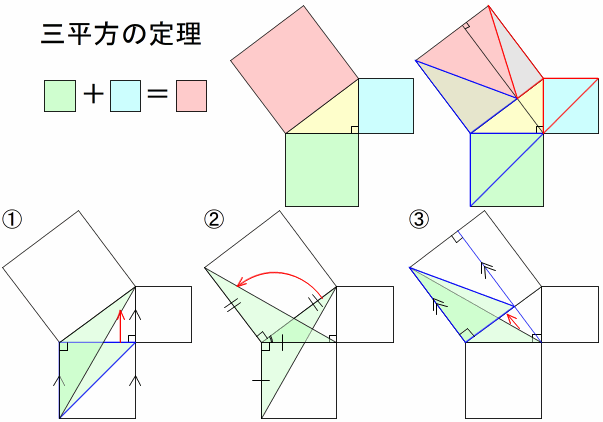



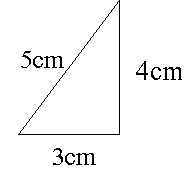
3 4 5の三角形で 本当に直角ができる Note Board




交流回路でよく使う三角形の比 電験三種講座の翔泳社アカデミー




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット




30 60 90 と 45 45 90 の直角三角形の辺の比 具体例で学ぶ数学



3



中学数学 三角形の内角と外角の関係の利用




iq問題 三角形の中にある法則で数字が並んでいます 法則がなりたつとしたら にはなにがくるのか Jyankquiz



三角形の性質



図形の扉 三角形の外角の定理




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



Lh3 Googleusercontent Com Proxy Vfni7q1hzkigrlnk8ixw Og8 Bojvi1xnvhcxpnm9up394gzdz4ttwrf Bzda Fwk 0lhgvsmpvvmyyfg73hoaqxqzmgizbjfsrzmswku1y Qoq Vtnegkkxj9kgqkv Kv8ucdmf55pf4bz9u87fe29gyqrxxsfxsukg5vaxhgdbxncmcxu




中学数学 中学流 に外接円の半径を求める ジャムと愉快な仲間たち 0名




三角形の決定条件と自由度 高校数学の美しい物語




三角形の法則を利用しよう Youtube



三角形の性質
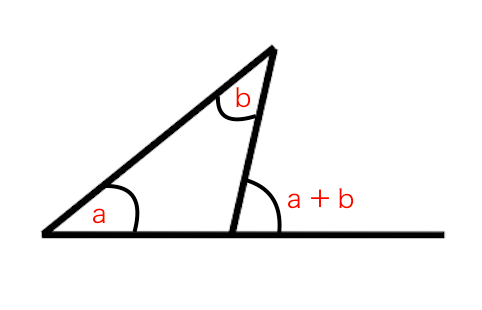



外角の定理とは 苦手な数学を簡単に




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




直角三角形の辺の長さ 合同条件 面積について アタリマエ




中3数学 3 4 5の直角三角形の辺の長さを求める3つの問題 Qikeru 学びを楽しくわかりやすく



七五三 三角形から円に内接する四角形へ




3分でわかる 三平方の定理 ピタゴラスの定理 の公式とは Qikeru 学びを楽しくわかりやすく
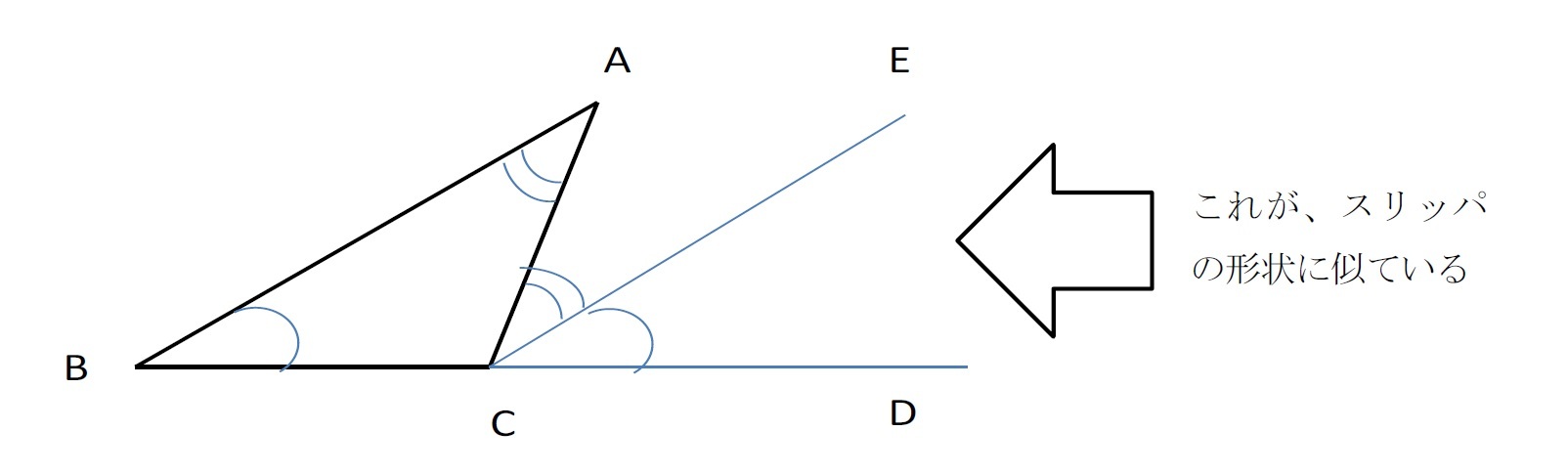



スリッパの法則 って 知っていますか ニッセイ基礎研究所




三角形の各辺が3 4 5のとき直角三角形である理由 図付き なぜか分かる はかせちゃんの怪しい研究室



1




3分で分かる 直角二等辺三角形の定義 性質 証明などについてわかりやすく 合格サプリ




三平方の定理 覚えること 三角定規 苦手な数学を簡単に
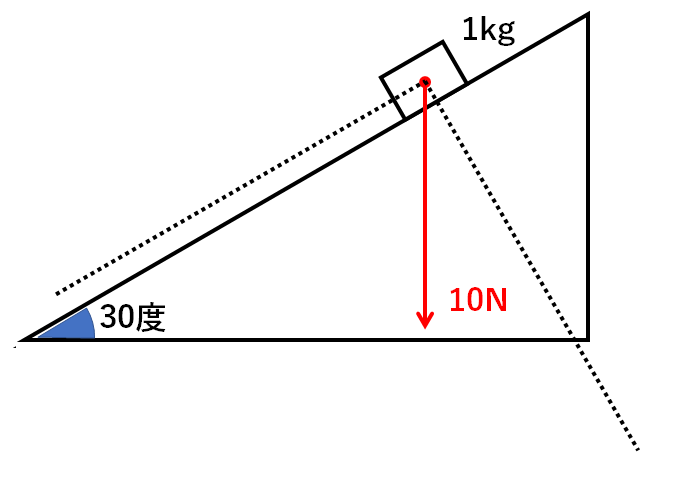



中3物理 分力と三平方の定理 中学理科 ポイントまとめと整理




中2数学 三角形 直角三角形の合同条件の覚え方のポイントを解説 まなビタミン



1




中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生



0 件のコメント:
コメントを投稿